题目内容
2．甲乙两人下棋，和棋的概率是$\frac{1}{2}$，乙获胜的概率是$\frac{1}{3}$，则甲不输的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
分析 根据甲输的概率是乙获胜的概率，甲不输与甲输是对立事件，求出对应的概率．
解答 解：甲乙两人下棋，记“甲不输”为事件A，“乙获胜”为事件B，
则P（B）=$\frac{1}{3}$；
又甲输的概率是乙获胜的概率，
且甲不输与甲输是对立事件，
所以甲不输的概率是
P（A）=1-P（B）=1-$\frac{1}{3}$=$\frac{2}{3}$．
故选：D．
点评 本题可惜了互斥事件与对立事件的概率公式的应用问题，是基础题目．
练习册系列答案
相关题目
12．
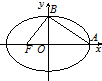如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{3}+1}}{2}$ | C． | $\frac{{\sqrt{5}+1}}{3}$ | D． | $\frac{{\sqrt{7}-1}}{2}$ |
13．在△ABC中，P是BC边中点，若$|{\overrightarrow{AB}}|\overrightarrow{AC}+|{\overrightarrow{BC}}|\overrightarrow{PA}+|{\overrightarrow{AC}}|\overrightarrow{PB}=\overrightarrow 0$，则△ABC的形状是（ ）
| A． | 等边三角形 | B． | 直角三角形 | ||
| C． | 等腰直角三角形 | D． | 等腰三角形但不一定是等边三角形 |
10．
如图，在棱长为2的正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，M、N分别是棱DD1、D1C1的中点，则直线OM（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，M、N分别是棱DD1、D1C1的中点，则直线OM（ ）| A． | 与AC、MN均垂直相交 | B． | 与AC垂直、与MN不垂直 | ||
| C． | 与MN垂直，与AC不垂直 | D． | 与AC、MN均不垂直 |