题目内容
已知a、b为正有理数,设m=
,n=
.
(Ⅰ)比较m、n的大小;
(Ⅱ)求证:
的大小在m、n之间.
| b |
| a |
| 2a+b |
| a+b |
(Ⅰ)比较m、n的大小;
(Ⅱ)求证:
| 2 |
(Ⅰ)m-n=
-
=
=
,
∵a、b为正有理数,∴b≠
a,
∴当b>
a时,m>n,当b<
a时,m<n.
(Ⅱ)∵m-
=
-
=
,n-
=
-
=
,
∴(m-
)(n-
)=-
<0,
因此,
的大小在m、n之间.
| b |
| a |
| 2a+b |
| a+b |
| b2-2a2 |
| a(a+b) |
(b+
| ||||
| a(a+b) |
∵a、b为正有理数,∴b≠
| 2 |
∴当b>
| 2 |
| 2 |
(Ⅱ)∵m-
| 2 |
| b |
| a |
| 2 |
b-
| ||
| a |
| 2 |
| 2a+b |
| a+b |
| 2 |
(
| ||||
| a+b |
∴(m-
| 2 |
| 2 |
(
| ||||
| a(a+b) |
因此,
| 2 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
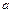 、
、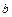 、
、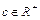 且
且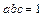 求证
求证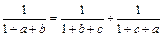 ≤1
≤1
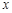 的不等式
的不等式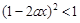 .
.