题目内容
下列不等式:
①x2+3>2x(x∈R)
②a3+b3≥a2b+ab2(a,b∈R)
③a2+b2≥2(a-b-1)
其中正确的个数有( )个.
①x2+3>2x(x∈R)
②a3+b3≥a2b+ab2(a,b∈R)
③a2+b2≥2(a-b-1)
其中正确的个数有( )个.
| A.0 | B.1 | C.2 | D.3 |
①x2+3-2x=(x-1)2+2>0,∴x2+3>2x成立.∴①正确.
②a3+b3-a2b-ab2=a2(a-b)+b2(b-a)=(a-b)(a2-b2)=(a-b)2(a+b),当a+b<0时,不等式a3+b3≥a2b+ab2不成立,∴②错误.
③a2+b2-2(a-b-1)=a2-2a+b2+2b+2=(a-1)2+(b+1)2≥0,∴a2+b2≥2(a-b-1)成立,即③正确.
故正确的是①③.
故选:C.
②a3+b3-a2b-ab2=a2(a-b)+b2(b-a)=(a-b)(a2-b2)=(a-b)2(a+b),当a+b<0时,不等式a3+b3≥a2b+ab2不成立,∴②错误.
③a2+b2-2(a-b-1)=a2-2a+b2+2b+2=(a-1)2+(b+1)2≥0,∴a2+b2≥2(a-b-1)成立,即③正确.
故正确的是①③.
故选:C.

练习册系列答案
相关题目
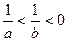 ,则下列不等式 ①
,则下列不等式 ①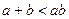 ;②
;②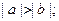 ③
③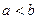 ;④
;④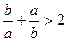 中,正确的不等式有 ( )
中,正确的不等式有 ( )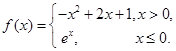 则满足
则满足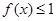 的实数
的实数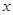 的取值范围是 .
的取值范围是 .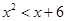 的解集为_____
的解集为_____