题目内容
已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.
(1)当M为空集时,求实数a的取值范围;
(2)如果M⊆[1,4],求实数a的取值范围.

(1)当M为空集时,求实数a的取值范围;
(2)如果M⊆[1,4],求实数a的取值范围.

(1)∵M为空集,
∴△=4a2-4(a+2)<0,即a2-a-2<0
∴实数a的取值范围为(-1,2)
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2,
①当M为空集,由(1)可得:a∈(-1,2)时,M⊆[1,4].
②当M不为空集时,
∵M⊆[1,4]
∴
即
,
解得1≤a≤
.
∴实数a的取值范围为[1,
].
综上得实数a的取值范[-1,
].
∴△=4a2-4(a+2)<0,即a2-a-2<0
∴实数a的取值范围为(-1,2)
(2)f(x)=x2-2ax+a+2=(x-a)2-a2+a+2,
①当M为空集,由(1)可得:a∈(-1,2)时,M⊆[1,4].
②当M不为空集时,
∵M⊆[1,4]
∴
|
即
|
解得1≤a≤
| 18 |
| 7 |
∴实数a的取值范围为[1,
| 18 |
| 7 |
综上得实数a的取值范[-1,
| 18 |
| 7 |

练习册系列答案
相关题目
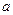 ,b是两个实数,且
,b是两个实数,且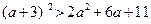 ;②
;②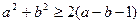 ;③
;③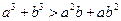 ;④
;④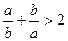 。上述4个式子中恒成立的有 ( )
。上述4个式子中恒成立的有 ( )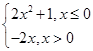 ,则不等式f(x)-x≤2的解集是________.
,则不等式f(x)-x≤2的解集是________.