题目内容
3.在△ABC中,角A、B、C成等差数列,b=$\sqrt{3}$,则△ABC的周长的最大值为( )| A. | 3$+\sqrt{3}$ | B. | 2$+\sqrt{3}$ | C. | 1$+2\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 由∠A、∠B、∠C的大小成等差数列,利用等差数列的性质及内角和定理求出B的度数,由b,sinB的值,利用正弦定理表示出a与c,设周长为y=a+b+c,将表示出的a与c,以及b的值代入,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可确定出△ABC的周长的最大值.
解答 解:∵A,B,C成等差数列,
∴A+C=2B=π-B,
解得:B=$\frac{π}{3}$,
∵b=$\sqrt{3}$,
∴$\frac{c}{sinC}=\frac{a}{sinA}=\frac{b}{sinB}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴c=2sinC,a=2sinA,
设周长为y,
则y=a+b+c=2sinA+2sinC+$\sqrt{3}$
=2sinA+2sin[π-($\frac{π}{3}$+A)]+$\sqrt{3}$
=2sinA+2sin(A+$\frac{π}{3}$)+$\sqrt{3}$
=2sinA+2sinAcos$\frac{π}{3}$+2cosAsin$\frac{π}{3}$+$\sqrt{3}$
=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$sinA+$\frac{1}{2}$cosA)+$\sqrt{3}$
=2$\sqrt{3}$sin(A+$\frac{π}{6}$)+$\sqrt{3}$,
∵0<A<$\frac{2π}{3}$,
∴$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$,即$\frac{1}{2}$<sin(A+$\frac{π}{6}$)≤1,
∴2$\sqrt{3}$<2$\sqrt{3}$sin(A+$\frac{π}{6}$)+$\sqrt{3}$≤3$\sqrt{3}$,
故选:D.
点评 此题考查了正弦定理,正弦函数的定义域与值域,等差数列的性质,熟练掌握正弦定理是解本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ($\frac{\sqrt{13}-1}{2}$,$\frac{\sqrt{13}+1}{2}$) | B. | ($\frac{1-\sqrt{13}}{2}$,$\frac{1+\sqrt{13}}{2}$) | C. | (-2,1) | D. | (-1,2) |
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
| A. | 关于x轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线y=x对称 | D. | 关于直线y=-x对称 |
 ,各项
,各项 ,公比为
,公比为 .(1)设
.(1)设 ,求证:
,求证: 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项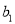 及公差
及公差 ;
; 的取值范围.
的取值范围.