题目内容
8.已知△ABC的内角A,B,C的对边分别为a,b,c,且$\frac{b-c}{a+c}$=$\frac{sinA}{sinB+sinC}$,则B=$\frac{2π}{3}$.分析 由正弦定理化简已知等式$\frac{b-c}{a+c}$=$\frac{sinA}{sinB+sinC}$=$\frac{a}{b+c}$,整理可得:a2+c2-b2=-ac,由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=-$\frac{1}{2}$,结合范围B∈(0,π)即可解得B的值.
解答 解:∵由正弦定理可得:sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,
∴$\frac{b-c}{a+c}$=$\frac{sinA}{sinB+sinC}$=$\frac{a}{b+c}$,整理可得:a2+c2-b2=-ac,
∴由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{-ac}{2ac}$=-$\frac{1}{2}$,
∴由B∈(0,π),可得:B=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.函数f(x),g(x)均为奇函数,定义域都为[-a,a](a>0),则f(g(x))为( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 无法判断奇偶性 |
16.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2ax+4a(x<1)}\\{(a-3)x+4a(x≥1)}\end{array}\right.$,满足对任意x1≠x2,都有 $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$] | C. | (0,1) | D. | [1,$\frac{4}{3}$] |
3.在△ABC中,角A、B、C成等差数列,b=$\sqrt{3}$,则△ABC的周长的最大值为( )
| A. | 3$+\sqrt{3}$ | B. | 2$+\sqrt{3}$ | C. | 1$+2\sqrt{3}$ | D. | 3$\sqrt{3}$ |
17.在锐角△ABC中,已知AB=2,∠B=2∠C,则AC的取值范围是( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{2}$) | C. | (2$\sqrt{2}$,4) | D. | (2,2$\sqrt{3}$) |
 中,
中,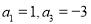 ,则
,则 ____________.
____________.