题目内容
18.当a>0且a≠1时,函数f(x)=ax+1-1的图象一定过点( )| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
分析 根据a0=1(a≠0),因此令x+1=0即可求出函数f(x)=ax+1-1的图象所过的定点坐标.
解答 解:当x+1=0,即x=-1时,
ax+1-1=0恒成立,
故函数f(x)=ax+1-1的图象一定过点(-1,0),
故选:C
点评 本题考查的知识点是指数函数的图象和性质,充分利用a0=1(a≠0)是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
3.在△ABC中,角A、B、C成等差数列,b=$\sqrt{3}$,则△ABC的周长的最大值为( )
| A. | 3$+\sqrt{3}$ | B. | 2$+\sqrt{3}$ | C. | 1$+2\sqrt{3}$ | D. | 3$\sqrt{3}$ |
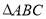 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知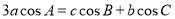 .
.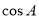 的值;
的值; ,求边
,求边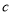 的值.
的值.