题目内容
已知等比数列 ,各项
,各项 ,公比为
,公比为 .(1)设
.(1)设 ,求证:
,求证:
(1)数列 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项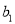 及公差
及公差 ;
;
(2)设(1)中的数列 单调递减,求公比
单调递减,求公比 的取值范围.
的取值范围.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在△ABC中,角A、B、C成等差数列,b=$\sqrt{3}$,则△ABC的周长的最大值为( )
| A. | 3$+\sqrt{3}$ | B. | 2$+\sqrt{3}$ | C. | 1$+2\sqrt{3}$ | D. | 3$\sqrt{3}$ |
1. 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
(Ⅰ)完成频率分布表,并画出频率分布直方图;
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.


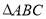 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知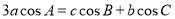 .
.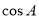 的值;
的值; ,求边
,求边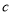 的值.
的值. 中,
中,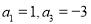 ,则
,则 ____________.
____________.