题目内容
20.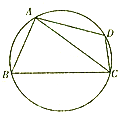 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.(1)请计算原棚户区ABCD的面积及圆面的半径R;
(2)因地理条件的限制,边界AD,CD不能变更,而边界AB、BC可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧ABC上求出一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.(注:圆的内接四边形对角互补)
分析 (1)连接AC,根据余弦定理求得cos∠ABC的值,进而求得∠ABC,然后利用三角形面积公式分别求得△ABC和△ADC的面积,二者相加即可求得四边形ABCD的面积,在△ABC中,由余弦定理求得AC,进而利用正弦定理求得外接圆的半径;
(2)设AP=x,CP=y.根据余弦定理求得x和y的关系式,进而根据均值不等式求得xy的最大值,进而求得△APC的面积的最大值,与△ADC的面积相加即可求得四边形APCD面积的最大值.
解答  解:(1)因为四边形ABCD内接于圆,
解:(1)因为四边形ABCD内接于圆,
所以∠ABC+∠ADC=180°,连接AC,由余弦定理:
AC2=42+62-2×4×6×cos∠ABC
=42+22-2×2×4cos∠ADC、
所以cos∠ABC=$\frac{1}{2}$,∵∠ABC∈(0°,180°),
故∠ABC=60°.
S四边形ABCD=$\frac{1}{2}$×4×6×sin60°+$\frac{1}{2}$×2×4×sin120°
=8$\sqrt{3}$(万平方米).
在△ABC中,由余弦定理:
AC2=AB2+BC2-2AB•BC•cos∠ABC
=16+36-2×4×6×$\frac{1}{2}$.
AC=2$\sqrt{7}$.
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=2R,
∴2R=$\frac{AC}{sin∠ABC}$=$\frac{2\sqrt{7}}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{21}}{3}$,
∴R=$\frac{2\sqrt{21}}{3}$(万米);
(2)∵S四边形APCD=S△ADC+S△APC,
又S△ADC=$\frac{1}{2}$AD•CD•sin120°=2$\sqrt{3}$,
设AP=x,CP=y.
则S△APC=$\frac{1}{2}$xy•sin60°=$\frac{\sqrt{3}}{4}$xy.
又由余弦定理AC2=x2+y2-2xycos60°
=x2+y2-xy=28.
∴x2+y2-xy≥2xy-xy=xy.
∴xy≤28,当且仅当x=y时取等号.
∴S四边形APCD=2$\sqrt{3}$+$\frac{\sqrt{3}}{4}$xy≤2$\sqrt{3}$+$\frac{\sqrt{3}}{4}$×28=9$\sqrt{3}$,
∴当P为圆弧ABC的中点时,四边形APCD的面积最大,且为9$\sqrt{3}$万平方米.
点评 本题主要考查了解三角形的实际应用,正弦定理和余弦定理的应用以及基本不等式求最值.考查了基础知识的综合运用.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 0.5 | B. | 3.5 | C. | 5.5 | D. | 6.5 |
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,-2) | B. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=(-$\frac{1}{2}$,$\frac{3}{4}$) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(1,-2),$\overrightarrow{{e}_{2}}$=(5,7) |
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | b>a>c |
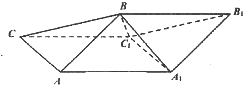 斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.
斜三棱柱ABC-A1B1C1中,侧面ABB1A1⊥侧面ACC1A1,A1B=AB=AA1=AC=2,四边形ACC1A1的面积为2$\sqrt{3}$,且∠AA1C1为锐角.