题目内容
7．已知2sinα+cosα=0，则2cos2α-sin2α的值为（ ）| A． | $\frac{12}{5}$ | B． | $\frac{5}{12}$ | C． | $\frac{6}{5}$ | D． | -2 |
分析 利用“1”的代换，化简所求的表达式，即可求出结果．
解答 解：2cos2α-sin2α=$\frac{{2cos}^{2}α-sin2α}{{sin}^{2}α+{cos}^{2}α}$=$\frac{{2cos}^{2}α-2sinαcosα}{{sin}^{2}α+{cos}^{2}α}$=$\frac{{8sin}^{2}α+4sinαsinα}{{sin}^{2}α+4{sin}^{2}α}$=$\frac{12}{5}$．
故选：A．
点评 本题考查二倍角公式以及同角三角函数的基本关系式的应用，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．一个四棱柱的底面是正方形，侧棱与底面垂直，其长度为4，棱柱的体积为16，棱柱的各顶点在一个球面上，则这个球的表面积是（ ）
| A． | 16π | B． | 20π | C． | 24π | D． | 32π |
12．复数z=$\frac{1}{2+i}$-i2015（i为虚数单位），则$\overline{z}$的虚部为（ ）
| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{4}{5}$i | D． | -$\frac{4}{5}$i |
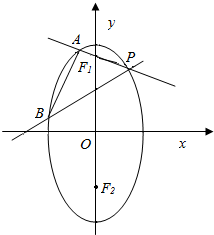已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$（a＞b＞0）的两个焦点分别为F1，F2，离心率为$\frac{{\sqrt{2}}}{2}$，直线$y=\sqrt{2}$过椭圆的焦点，点P是椭圆上位于第一象限的点，并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$，过P作倾斜角互补的两条直线PA，PB分别交椭圆于A，B两点．