题目内容
(本小题满分10分)(选修4-1:几何证明选讲)
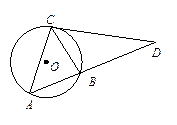
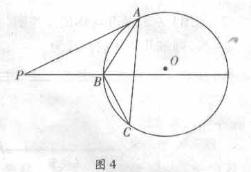
如图: 是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。

(1)求证: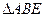
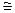
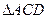 ;
;
(2)若AB=6,BC=4,求AE。
如图:
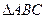 是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
(1)求证:
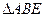
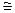
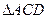 ;
;(2)若AB=6,BC=4,求AE。
(1)
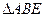
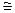
 ,证明略。
,证明略。(2)
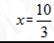
解:(I)在△ABC和△ACD中,
∵AB="AC " ∠ABC=∠ACD ……(2分)
又∠BAE=∠EDC
∵BD//MN
∴∠EDC=∠DCN
∵直线是圆的切线
∴∠DCN=∠CAD
∴∠BAE=∠CAD
∴△ABE≌△ACD(SAS) ……(5分)
(II)∵∠EBC=∠BCM ∠BCM=∠BDC
∴∠EBC=∠BDC=∠BAC BC=CD=4
又∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB
∴BC="BE=4 " ……(7分)
设AE="x." 易证△ABE∽△DEC
∴
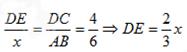
又AE·EC=BE·ED EC=6-x
∴
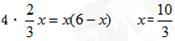 ……(10分)
……(10分)
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
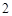 ,四边形
,四边形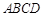 中,
中,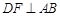 ,垂足为
,垂足为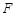 ,
,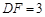 ,
,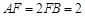 ,延长
,延长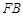 到
到 ,使
,使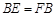 , 连结
, 连结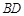 ,
,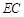 .若
.若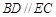 ,则四边形
,则四边形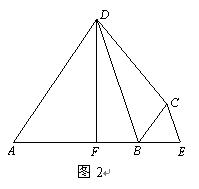



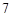

 E是BC上任意一点,EF⊥AB于F。
E是BC上任意一点,EF⊥AB于F。
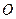 外一点
外一点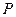 分别作圆
分别作圆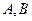 。且
。且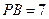 ,
,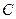 是圆上一点使得
是圆上一点使得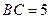 ,
,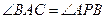 ,则
,则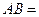 .
.
 长AB和DC相交于点P. 若PB=2,PD=6,则
长AB和DC相交于点P. 若PB=2,PD=6,则 的值为 。
的值为 。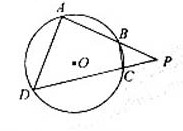
 是
是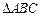 的外接圆,过点
的外接圆,过点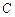 的切线交
的切线交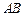 的延长线于点
的延长线于点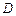 ,
,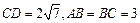 ,则
,则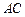 的长为 .
的长为 .