题目内容
【题目】已知函数f(x)![]() ,g(x)=|xlnx﹣ax2|,a
,g(x)=|xlnx﹣ax2|,a![]() .
.
(1)讨论f(x)的单调性;
(2)若g(x)在区间(1,e)有极小值,求a的取值范围.
【答案】(1) x∈(0,e)时, f(x)单调递增;x∈(e,+∞)时,函数f(x)单调递减. (2) a∈![]() .
.
【解析】
(1)利用导数的符号可得单调性;
(2)根据(1) 可得:![]() ,结合a
,结合a![]() ,可得g(x)=ax2﹣xlnx.a
,可得g(x)=ax2﹣xlnx.a![]() .x∈(1,e).通过两次求导后,讨论
.x∈(1,e).通过两次求导后,讨论![]() 可得结果.
可得结果.
(1)函数f(x)![]() ,x∈(0,+∞).
,x∈(0,+∞).
f′(x)![]() .
.
∴x∈(0,e)时,f′(x)>0,此时函数f(x)单调递增;x∈(e,+∞)时,f′(x)<0,此时函数f(x)单调递减.
(2)由(1)可得:![]() .
.
g(x)=|xlnx﹣ax2|,a![]() .x∈(1,e).
.x∈(1,e).
∴![]() |
|![]() a|=a
a|=a![]() ,
,
∴g(x)=ax2﹣xlnx.a![]() .x∈(1,e).
.x∈(1,e).
g′(x)=2ax﹣lnx﹣1=h(x),
h′(x)=2a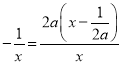 .
.
①![]() 时,1
时,1![]() e.此时x
e.此时x![]() 时,函数h(x)取得极小值,h(
时,函数h(x)取得极小值,h(![]() )=ln
)=ln![]() ln(2a)<0.
ln(2a)<0.
h(1)=2a﹣1<0,h(e)=2ae﹣2>0.
∴存在x0∈(![]() ,e),使得g′(x0)=2ax0﹣lnx0﹣1=0,
,e),使得g′(x0)=2ax0﹣lnx0﹣1=0,
此时,函数g(x)在(1,x0)上单调递减,在(x0,e)上单调递增.
即此时g(x)在区间(1,e)有极小值,a的取值范围为a∈![]() .
.
②a![]() 时,0
时,0![]() 1.h′(x)>0,函数h(x)在(1,e)上单调递增,h(1)=2a﹣1≥0,
1.h′(x)>0,函数h(x)在(1,e)上单调递增,h(1)=2a﹣1≥0,
∴g′(x)>0,∴函数g(x)在(1,e)上单调递增,无极值,舍去.

练习册系列答案
相关题目