题目内容
【题目】正三棱锥
，
为
中点， 
，
，过的平面截三棱锥的外接球所得截面的面积范围为（ ）
A.
B.
C.
D.
【答案】D
【解析】
根据题中数据，结合正棱锥的结构特征，得到
两两垂直，可将正三棱锥
看作正方体的一角，设正方体的体对角线的中点为
，得到点是正三棱锥外接球的球心，记外接球半径为
，过球心的截面圆面积最大；再求出
，根据球的结构特征可得，当
垂直于过
的截面时，截面圆面积最小，结合题中数据，即可求出结果.
因为正三棱锥，
，
，
所以
，即
，同理
，
，
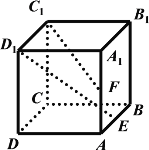
因此正三棱锥可看作正方体的一角，如图，
记正方体的体对角线的中点为，由正方体结构特征可得，点即是正方体的外接球球心，
所以点也是正三棱锥外接球的球心，记外接球半径为，
则
，
因为球的最大截面圆为过球心的圆，
所以过的平面截三棱锥的外接球所得截面的面积最大为
；
又为
中点，由正方体结构特征可得
；
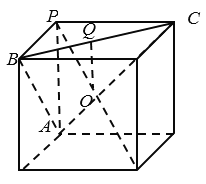
由球的结构特征可知，当垂直于过的截面时，截面圆半径最小为
，
所以
.
因此，过的平面截三棱锥的外接球所得截面的面积范围为
.
故选：D.
练习册系列答案
津桥教育计算小状元系列答案
相关题目
