题目内容
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,
, ![]() ,则称
,则称![]() 为“D-数列”.
为“D-数列”.
(1)举出一个前六项均不为零的“D-数列”(只要求依次写出该数列的前六项);
(2)若“D-数列”![]() 中,
中,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,分别判断当
,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值(若不存在不需要交代理由);
的极限是否存在?如果存在,求出其极限值(若不存在不需要交代理由);
(3)证明:任何“D-数列”中总含有无穷多个为零的项.
【答案】(1)![]() (2)
(2)![]() 的极限不存在.
的极限不存在.![]() 的极限存在.极限值为6 (3)见解析
的极限存在.极限值为6 (3)见解析
【解析】
(1)举出一个例子即可
(2)![]() 的极限不存在.
的极限不存在.![]() 的极限存在,计算得到
的极限存在,计算得到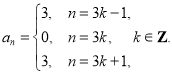 ,
,![]() 得到答案.
得到答案.
(3)假设![]() 中只有有限个零, 则存在
中只有有限个零, 则存在![]() , 使得当
, 使得当![]() 时,
时, ![]() ,当
,当![]() 时, 记
时, 记![]() ,计算得到
,计算得到![]() 形成了一列严格递减的无穷正整数数列,不能成立,得到证明.
形成了一列严格递减的无穷正整数数列,不能成立,得到证明.
(1)![]()
(2)![]() 的极限不存在.
的极限不存在.![]() 的极限存在.
的极限存在.
事实上, 因为![]() ,
, ![]() ,
, ![]() , 当
, 当![]() 时,
时, 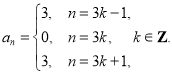 .因此当
.因此当![]() 时,
时, ![]() .所以
.所以![]() .
.
(3) 反证法, 假设![]() 中只有有限个零, 则存在
中只有有限个零, 则存在![]() , 使得当
, 使得当![]() 时,
时, ![]() .
.
当![]() 时, 记
时, 记![]()
于是![]() ,
, ![]() , 故
, 故![]() ,
,
而![]() , 从而
, 从而![]() .
.
这样![]() 形成了一列严格递减的无穷正整数数列, 这不可能,故假设不成立,
形成了一列严格递减的无穷正整数数列, 这不可能,故假设不成立, ![]() 中必有无限个
中必有无限个![]() .
.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()