题目内容
8.已知f(x+2)=${3}^{{x}^{2}+4x+4}$(1)求函数f(x)的解析式
(2)判断函数f(x)的奇偶性
(3)解不等式f(x-2)>f(x+3)
分析 (1)根据题意,f(x+2)=${3}^{{x}^{2}+4x+4}$=${3}^{(x+2)^{2}}$,利用换元法令t=x+2,则x=t-2,代入f(x)中即可得答案;
(2)根据题意,先求出f(x)=${3}^{{x}^{2}}$的定义域为R,进而求出又由于f(-x)=${3}^{{x}^{2}}$,分析f(-x)与f(x)的关系即可得答案;
(3)由函数的解析式可将f(x-2)>f(x+3)转化为${3}^{(x-2)^{2}}$>${3}^{(x+3)^{2}}$,再由指数函数的性质可得(x+2)2>(x+3)2,解可得答案.
解答 解:(1)根据题意,f(x+2)=${3}^{{x}^{2}+4x+4}$=${3}^{(x+2)^{2}}$,
令t=x+2,则x=t-2,
则f(t)=${3}^{{t}^{2}}$,
故f(x)=${3}^{{x}^{2}}$;
(2)由(1)可得,f(x)=${3}^{{x}^{2}}$,易得其定义域为R,
又由于f(-x)=${3}^{{x}^{2}}$=f(x),
故f(x)为偶函数;
(3)若f(x-2)>f(x+3),
即${3}^{(x-2)^{2}}$>${3}^{(x+3)^{2}}$,
即(x+2)2>(x+3)2,
解可得:x<-$\frac{1}{2}$.
点评 本题考查指函数奇偶性的运用涉及指数函数的性质,解题的关键是正确求出f(x)的解析式.

练习册系列答案
相关题目
3.已知全集U={1,2,3,4,5,6,7,8},集合A={1,4,7},集合B={1,3,4,6,8},则(∁UA)∩B=( )
| A. | {1,4} | B. | {3,6,8} | C. | {1,2,4,5,7} | D. | {2,3,5,6,7,8} |
13.甲、乙两车从A地沿同一路线到达B地,甲车一半时间的速度为a,另一半时间的速度为b,乙车用速度a行走了一半路程,用速度b行走了另一半路程,若a≠b,则两车到达B地的情况是( )
| A. | 甲车先到达B地 | B. | 甲车先到达B地 | C. | 同时到达 | D. | 不能判断 |
18.已知三棱锥P-ABC的底面△ABC是正三角形,且PA=PB=PC,E、F是棱PA、BC的中点,记EF与平面PAB所成的角为α,EF与平面ABC所成的角为β,则α+β( )
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | ||
| C. | 大于$\frac{π}{2}$ | D. | 与$\frac{π}{2}$的大小关系不能确定 |
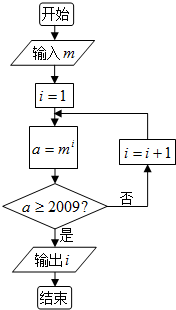 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)