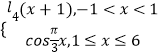题目内容
【题目】已知圆C的方程为：x2+y2=4
（1）求过点P（2，1）且与圆C相切的直线l的方程；
（2）直线l过点D（1，2），且与圆C交于A、B两点，若|AB|=2 
，求直线l的方程；
（3）圆C上有一动点M（x0 ， y0）， 
=（0，y0），若向量 
= 
+ ，求动点Q的轨迹方程．
【答案】
（1）解：当k不存在时，x=2满足题意；
当k存在时，设切线方程为y﹣1=k（x﹣2），
由 
=2得，k=﹣ 
，
则所求的切线方程为x=2或3x+4y﹣10=0
（2）解：当直线l垂直于x轴时，此时直线方程为x=1，l与圆的两个交点坐标为（1， 
）和（1，﹣ ），这两点的距离为2 ，满足题意；
当直线l不垂直于x轴时，设其方程为y﹣2=k（x﹣1），即kx﹣y﹣k+2=0，
设圆心到此直线的距离为d，
∴d= 
=1，即 
=1，
解得：k= ，
此时直线方程为3x﹣4y+5=0，
综上所述，所求直线方程为3x﹣4y+5=0或x=1
（3）解：设Q点的坐标为（x，y），
∵M（x0，y0）， 
=（0，y0）， 
= 
+ ，
∴（x，y）=（x0，2y0），
∴x=x0，y=2y0，
∵x02+y02=4，
∴x2+（ 
）2=4，即 
+ 
=1
【解析】（1）分两种情况考虑：当直线l的斜率不存在时，直线x=2满足题意；当k存在时，变形出l方程，利用圆心到l的距离d=r列出方程，求出方程的解得到k的值，确定出此时l方程，综上，得到满足题意直线l的方程；（2）分两种情况考虑：当直线l垂直于x轴时，此时直线方程为x=1，直线l与圆的两个交点距离为2 ，满足题意；
当直线l不垂直于x轴时，设其方程为y﹣2=k（x﹣1），求出圆心到直线l的距离d=1，利用点到直线的距离公式列出关于k的方程，求出方程的解得到k的值，确定出此时直线方程，综上，得到满足题意直线l的方程；（3）设Q（x，y），表示出 ， ，代入已知等式中化简得到x=x0 ， y=2y0 ， 代入圆方程变形即可得到Q轨迹方程．
