题目内容
【题目】如图，在五面体ABCDEF中，四边形ABCD是边长为2的正方形，EF∥平面ABCD，EF=1，FB=FC，∠BFC=90°，AE= 
，H是BC的中点． 
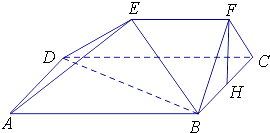
（1）求证：FH∥平面BDE；
（2）求证：AB⊥平面BCF；
（3）求五面体ABCDEF的体积．
【答案】
（1）证明：连接AC，AC与BD相交于点O，则点O是AC的中点，连接OH，EO，
∵H是BC的中点，
∴OH∥AB， 
∵EF∥平面ABCD，EF平面ABFE，平面ABCD∩平面ABFE=AB，
∴EF∥AB．
∵EF=1，
∴OH∥EF，OH=EF．
∴四边形EOHF是平行四边形．
∴EO∥FH，EO=FH．
∵EO平面BDE，FH平面BDE，
∴FH∥平面BDE
（2）证明：取AB的中点M，连接EM，则AM=MB=1，
由（1）知，EF∥MB，且EF=MB，
∴四边形EMBF是平行四边形．
∴EM∥FB，EM=FB．
在Rt△BFC中，FB2+FC2=BC2=4，又FB=FC，得 
．
∴ 
．
在△AME中， 
，AM=1， ，
∴AM2+EM2=3=AE2．
∴AM⊥EM．
∴AM⊥FB，即AB⊥FB．
∵四边形ABCD是正方形，
∴AB⊥BC．
∵FB∩BC=B，FB平面BCF，BC平面BCF，
∴AB⊥平面BCF
（3）解：连接EC，
在Rt△BFC中， 
，
∴EO=FH=1．
由（2）知AB⊥平面BCF，且EF∥AB，
∴EF⊥平面BCF．
∵FH⊥平面ABCD，EO∥FH，
∴EO⊥平面ABCD．
∴四棱锥E﹣ABCD的体积为V1═ 
．
∴三棱锥E﹣BCF的体积为 
= 
．
∴五面体ABCDEF的体积为 
．
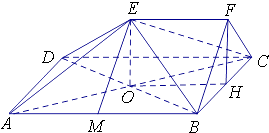
【解析】（1）设AC与BD交于点O，则点O是AC的中点，连接OH，EO，通过证明四边形EOHF是平行四边形，证明FH∥平面EDB；（2）先证明出四边形EMBF是平行四边形，推断出EM∥FB，EM=FB．进而在Rt△BFC中求得EM，在△AEM中，根据边长推断出AM2+EM2=3=AE2 ， 进而证明出AM⊥EM．然后证明出四边形ABCD是正方形，进而推断出AB⊥BC．最后通过线面垂直的判定定理证明出AB⊥平面BCF；（3）求出四棱锥E﹣ABCD的体积为V1═ 
，三棱锥E﹣BCF的体积为 = ，即可求出五面体ABCDEF的体积．
【考点精析】利用直线与平面平行的判定和直线与平面垂直的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．
