题目内容
【题目】已知△ABC，|AB|=8，AC与BC边所在直线的斜率之积为定值m，
（1）求动点C的轨迹方程；
（2）当m=1时，过点E（0，1）的直线l与曲线C相交于P、Q两点，求P、Q两点的中点M的轨迹方程．
【答案】
（1）解：以AB边所在直线为x轴，以AB边的垂直平分线为y轴建立平面直角坐标系
则A（﹣4，0），B（4，0）
设点C的坐标为（x，y），则 
，
∴ 
，
即mx2﹣y2=16m
当m=0时，动点C的轨迹方程为y=0（x≠±4），
表示x轴所在直线去掉A、B两点剩下的部分
当m＞0时，动点C的轨迹方程为 
表示焦点在x轴上的双曲线去掉A、B两点剩下的部
当﹣1＜m＜0时，动点C的轨迹方程为 
表示焦点在x轴上的椭圆去掉A、B两点剩下的部分
当m＜﹣1时，动点C的轨迹方程为 
表示焦点在y轴上的椭圆去掉A、B两点剩下的部分
当m=﹣1时，动点C的轨迹方程为 x2+y2=16（x≠±4）
表示以AB为直径的圆去掉A、B两点剩下的部分
（2）解：当m=1时，动点C的轨迹方程为 ，
当直线l的斜率不存在时，显然不可能与 有交点，舍去；
当直线l的斜率存在时，设l的方程为y=kx+1，设P（x1，y1），Q（x2，y2），M（x0，y0）
联立方程组 
，
消去y得：（1﹣k2）x2﹣2kx﹣17=0
由题意得：x1、x2是此方程的解
所以 
∴ 
所以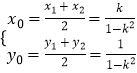 
，所以得 
又直线l与动点C的轨迹方程有两个不同的焦点，
则 
∴ 
且 
且k2≠1，∴ 
或y0＜﹣16
所以P、Q两点的中点M的轨迹方程为 
【解析】（1）以AB边所在直线为x轴，以AB边的垂直平分线为y轴建立平面直角坐标系，利用AC与BC边所在直线的斜率之积为定值m，建立方程，即可求动点C的轨迹方程；（2）分类讨论，联立方程组，即可求P、Q两点的中点M的轨迹方程．
