题目内容
已知函数f(x)=x2-(2a+1)x+alnx.
(Ⅰ)当a=1时,求函数f(x)的单调增区间;
(Ⅱ)求函数f(x)在区间[1,e]上的最小值;
(Ⅲ)设g(x)=(1-a)x,若存在x0∈[
,e],使得f(x0)≥g(x0)成立,求实数a的取值范围.
(Ⅰ)当a=1时,求函数f(x)的单调增区间;
(Ⅱ)求函数f(x)在区间[1,e]上的最小值;
(Ⅲ)设g(x)=(1-a)x,若存在x0∈[
| 1 |
| e |
f(x)的定义域为x>0
(I)将a=1代入f(x)得f(x)=)=x2-3x+lnx
所以f′(x)=2x-3+
=
令f′(x)>0得0<x<
或x>1
所以函数的单调增区间(0,
),(1,+∞)
(II)f′(x)=2x-(2a+1)+
=
令f′(x)=0得x=
(舍)或x=a
当a≤1时,在区间[1,e]上,f′(x)>0
f(x)在区间[1,e]上的单调递增
所以[f(x)]min=f(1)=-2a;
当1<a<e时,f(x)在[1,a]单调递减,在[a,e]上单调递增
所以[f(x)]min=f(a)=-a2-a+alna;
当a≥e时,f(x)在[1,e]上单调递减
所以[f(x)]min=f(e)=e2-2ae-e+a.
(III)令x2-(a+2)x+alnx≥0在[
,e]上有解.
即x2-2x≥a(x-lnx),由于x-lnx在[
,e]上为正数
∴问题转化为a≤
在[
,e]上有解
令h(x)=
,下求此函数在[
,e]的最大值
由于当x<2时,h(x)为负,下研究h(x)在(2,e)上的单调性,
由于h′(x)=
>0成立,所以h(x)=
在(2,e)上是增函数,又h(e)=
>0
所以h(x)max=
故实数a的取值范围为a≤
(I)将a=1代入f(x)得f(x)=)=x2-3x+lnx
所以f′(x)=2x-3+
| 1 |
| x |
| 2x2-3x+1 |
| x |
令f′(x)>0得0<x<
| 1 |
| 2 |
所以函数的单调增区间(0,
| 1 |
| 2 |
(II)f′(x)=2x-(2a+1)+
| a |
| x |
| 2x2-(2a+1)x+a |
| x |
令f′(x)=0得x=
| 1 |
| 2 |
当a≤1时,在区间[1,e]上,f′(x)>0
f(x)在区间[1,e]上的单调递增
所以[f(x)]min=f(1)=-2a;
当1<a<e时,f(x)在[1,a]单调递减,在[a,e]上单调递增
所以[f(x)]min=f(a)=-a2-a+alna;
当a≥e时,f(x)在[1,e]上单调递减
所以[f(x)]min=f(e)=e2-2ae-e+a.
(III)令x2-(a+2)x+alnx≥0在[
| 1 |
| e |
即x2-2x≥a(x-lnx),由于x-lnx在[
| 1 |
| e |
∴问题转化为a≤
| x2-2x |
| x-lnx |
| 1 |
| e |
令h(x)=
| x2-2x |
| x-lnx |
| 1 |
| e |
由于当x<2时,h(x)为负,下研究h(x)在(2,e)上的单调性,
由于h′(x)=
| (x-1)(x+2-2lnx) |
| (x-lnx)2 |
| x2-2x |
| x-lnx |
| e2-2e |
| e-1 |
所以h(x)max=
| e2-2e |
| e-1 |
故实数a的取值范围为a≤
| e2-2e |
| e-1 |

练习册系列答案
相关题目
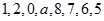 的中位数为
的中位数为 ,则直线
,则直线 与曲线
与曲线 围成图形的面积为 .
围成图形的面积为 .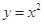 在
在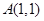 处的切线与
处的切线与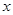 轴及该抛物线所围成的图形面积为 .
轴及该抛物线所围成的图形面积为 .