题目内容
已知可导函数f（x）（x∈R）的导函数f′（x）满足f′（x）＞f（x），则不等式ef（x）＞f（1）ex的解集是______．
令g（x）=
，
则g′(x)=
=
，
因为f'（x）＞f（x），所以g′（x）＞0，
所以，函数g（x）=
为（-∞，+∞）上的增函数，
由ef（x）＞f（1）ex，得：
＞
，即g（x）＞g（1），
因为函数g（x）=
为（-∞，+∞）上的增函数，
所以，x＞1．
所以，不等式ef（x）＞f（1）ex的解集是（1，+∞）．
故答案为（1，+∞）．
| f(x) |
| ex |
则g′(x)=
| ex•f′(x)-ex•f(x) |
| e2x |
| ex(f′(x)-f(x)) |
| e2x |
因为f'（x）＞f（x），所以g′（x）＞0，
所以，函数g（x）=
| f(x) |
| ex |
由ef（x）＞f（1）ex，得：
| f(x) |
| ex |
| f(1) |
| e |
因为函数g（x）=
| f(x) |
| ex |
所以，x＞1．
所以，不等式ef（x）＞f（1）ex的解集是（1，+∞）．
故答案为（1，+∞）．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
（
）
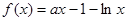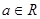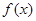的单调性；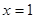
处取得极值，不等式
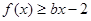对任意
恒成立，求实数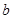
的取值范围；
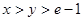时，证明不等式 
.
，
，
，
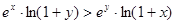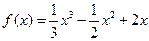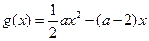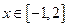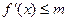恒成立，求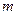
的最小值；
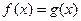在区间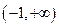
有三个不同的实根，求
的取值范围．