题目内容
已知定义在R上的函数f(x),g(x)满足f(x)g(x)=ax,且f′(x)g(x)+f(x)•g′(x)<0,f(1)g(1)+f(-1)g(-1)=
,若有穷数列{f(n)g(n)}(n∈N*)的前n项和等于
,则n等于______.
| 10 |
| 3 |
| 40 |
| 81 |
由(f(x)g(x))′=f′(x)g(x)+f(x)•g′(x)<0,
即axlna<0,故0<a<1.
由f(1)g(1)+f(-1)g(-1)=
,
得a+
=
,解得a=
,
∴有穷数列{f(n)g(n)}(n∈N*)是等比数列,其前n项和Sn=
=
,
得n=4.
故答案为:4.
即axlna<0,故0<a<1.
由f(1)g(1)+f(-1)g(-1)=
| 10 |
| 3 |
得a+
| 1 |
| a |
| 10 |
| 3 |
| 1 |
| 3 |
∴有穷数列{f(n)g(n)}(n∈N*)是等比数列,其前n项和Sn=
| ||||
1-
|
| 40 |
| 81 |
得n=4.
故答案为:4.

练习册系列答案
相关题目
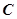 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积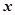 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是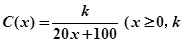 为常数).记
为常数).记 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.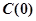 的实际意义,并建立
的实际意义,并建立 在区间
在区间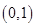 上单调递增,且方程
上单调递增,且方程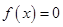 的根都在区间
的根都在区间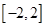 上,则实数b的取值范围为( )
上,则实数b的取值范围为( )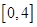

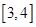
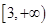
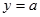 与函数
与函数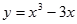 的图像有三个相异的交点,则
的图像有三个相异的交点,则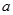 的取值范围为( )
的取值范围为( )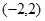
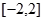
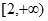

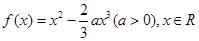
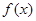 的单调区间和极值;
的单调区间和极值;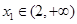 ,都存在
,都存在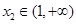 ,使得
,使得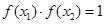 ,求
,求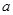 的取值范围
的取值范围