题目内容
18.函数y=log${\;}_{\frac{1}{2}}$(-x2+2x)的单调递增区间是 ( )| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
分析 先求该函数的定义域,可以看出原函数是由t=-x2+2x和$y=lo{g}_{\frac{1}{2}}t$复合而成,而$y=lo{g}_{\frac{1}{2}}t$在定义域内单调递减,从而找函数t=-x2+2x在原函数定义域内的单调减区间,便可得出原函数的单调递增区间.
解答 解:解-x2+2x>0得,0<x<2;
令t=-x2+2x,该函数的对称轴为x=1,∴该函数的单调减区间为(1,2);
又函数$y=lo{g}_{\frac{1}{2}}t$为减函数,原函数是由t=-x2+2x和$y=lo{g}_{\frac{1}{2}}t$复合而成;
∴原函数的单调递增区间为(1,2).
故选:D.
点评 考查对数函数的单调性,二次函数的单调性,及复合函数的定义,二次函数以及复合函数单调区间的求法.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
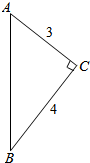 如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.
如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.