题目内容
3.已知函数f(x-3)=loga$\frac{x}{6-x}$(a>0,a≠1).(1)判断f(x)的奇偶性,并说明理由;
(2)当0<a<1时.求函数f(x)的单调区间.
分析 (1)换元,令x-3=t,可求t的范围:-3<t<3,这样便得到f(t)=$lo{g}_{a}\frac{t+3}{3-t}$,从而得出f(x),并求f(-x),这样即可判断f(x)的奇偶性;
(2)函数f(x)=$lo{g}_{a}\frac{x+3}{3-x}$是由函数u=$\frac{x+3}{3-x}$和y=logau复合而成,根据a的范围可判断y=logau为减函数,从而判断$u=\frac{x+3}{3-x}$在(-3,3)上单调性,并求其单调区间便可得出函数f(x)的单调区间.
解答 解:(1)令x-3=t,-3<t<3,则x=t+3;
f(t)=$lo{g}_{a}\frac{t+3}{3-t}$;
∴$f(x)=lo{g}_{a}\frac{x+3}{3-x},-3<x<3$;
∴$f(-x)=lo{g}_{a}\frac{3-x}{3+x}=-lo{g}_{a}\frac{x+3}{3-x}=-f(x)$;
∴f(x)为奇函数;
(2)令u=$\frac{x+3}{3-x}$=$\frac{-(3-x)+6}{3-x}$=$-1+\frac{6}{3-x}$,该函数在(-3,3)上为增函数;
又0<a<1;
∴函数logau为减函数;
∴复合函数f(x)单调减区间为(-3,3).
点评 考查换元法求函数解析式,奇函数的定义,以及根据奇偶函数的定义判断函数奇偶性的方法,复合函数的定义,对数函数的单调性,复合函数单调性的判断方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.函数y=log${\;}_{\frac{1}{2}}$(-x2+2x)的单调递增区间是 ( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
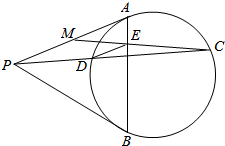 如图,过圆外一点P分别作⊙O的两条切线PA,PB和一条割线PDC,记PA的中点为M,连接CM与AB交于点E.求证:DE∥PA.
如图,过圆外一点P分别作⊙O的两条切线PA,PB和一条割线PDC,记PA的中点为M,连接CM与AB交于点E.求证:DE∥PA.