题目内容
5.已知各项均为正数的数列{an}前n项和为Sn,首项为a1,且$\frac{1}{2}$,an,Sn是等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若an2=($\frac{1}{2}$)${\;}^{{b}_{n}}$,设cn=$\frac{{b}_{n}}{{a}_{n}}$+(-1)nan,求数列{cn}的前n项和Tn.
分析 (Ⅰ)由题意知2an=$\frac{1}{2}$+Sn,当n=1时,得a1=$\frac{1}{2}$;当n≥2时,Sn=2an-$\frac{1}{2}$,Sn-1=2an-1-$\frac{1}{2}$,两式相减得an=Sn-Sn-1=2an-2an-1,由此能求出数列{an}的通项公式.
(Ⅱ)由an2=($\frac{1}{2}$)${\;}^{{b}_{n}}$,知bn=4-2n,由此利用错位相减法和等比数列的求和公式,能求出数列{cn}的前n项和Tn.
解答 解:(Ⅰ)由题意知2an=$\frac{1}{2}$+Sn,
当n=1时,2a1=a1+$\frac{1}{2}$,解得a1=$\frac{1}{2}$,
当n≥2时,Sn=2an-$\frac{1}{2}$,Sn-1=2an-1-$\frac{1}{2}$,
两式相减得an=Sn-Sn-1=2an-2an-1,
整理得:$\frac{{a}_{n}}{{a}_{n-1}}$=2,
∴数列{an}是以$\frac{1}{2}$为首项,2为公比的等比数列.
∴an=a1•2n-1=2n-2;
(Ⅱ)由an2=22n-4=($\frac{1}{2}$)${\;}^{{b}_{n}}$,
∴bn=4-2n,
∴cn=$\frac{{b}_{n}}{{a}_{n}}$+(-1)nan=$\frac{2-n}{{2}^{n-3}}$+(-1)n•2n-2.
由T'n=$\frac{2-1}{{2}^{-2}}$+$\frac{2-2}{{2}^{-1}}$+$\frac{2-3}{{2}^{0}}$+…+$\frac{2-n}{{2}^{n-3}}$,
$\frac{1}{2}$T'n=$\frac{2-1}{{2}^{-1}}$+$\frac{2-2}{{2}^{0}}$+$\frac{2-3}{{2}^{1}}$+…+$\frac{2-n}{{2}^{n-2}}$,
两式相减可得,$\frac{1}{2}$T'n=4-(2+1+$\frac{1}{2}$+…+$\frac{1}{{2}^{n-3}}$)-$\frac{2-n}{{2}^{n-2}}$,
$\frac{1}{2}$T'n=4-$\frac{2(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-$\frac{2-n}{{2}^{n-2}}$,
化简可得T'n=$\frac{n}{{2}^{n-3}}$,
即有Tn=T'n-$\frac{1}{2}$•$\frac{1-(-2)^{n}}{1-(-2)}$=$\frac{n}{{2}^{n-3}}$-$\frac{1-(-2)^{n}}{6}$.
点评 本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意错位相减法的合理运用.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | 1 | B. | 1或±$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
| A. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ](k∈Z) | B. | [$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{4}$+2kπ,$\frac{3π}{4}$+2kπ](k∈Z) | D. | [$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ](k∈Z) |
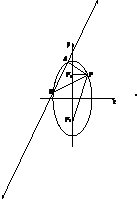 已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.
已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.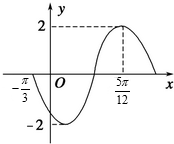
 如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论: