题目内容
10．已知ABCD-A1B1C1D1是边长为1的正方体，P为线段AB1上的动点，Q为底面ABCD上的动点，则PC1+PQ最小值为（ ）| A． | $1+\frac{{\sqrt{2}}}{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\frac{{1+\sqrt{5}}}{2}$ |
分析 如图所示，把上图中的△ABB1延AB1上转90°，得到下图，当C1Q⊥AB时，PC1+PQ=CQ最小．
解答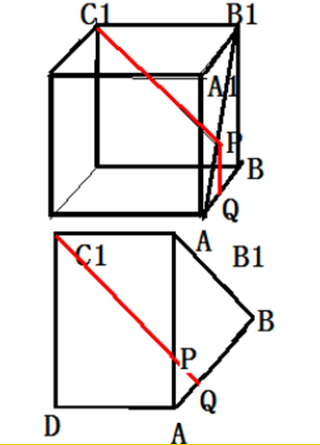 
解：如图所示，把上图中的△ABB1沿AB1上转90°，得到下图，当C1Q⊥AB时，PC1+PQ=CQ最小，
PC1=$\sqrt{2}$，PA=$\sqrt{2}$-1，PQ=$\frac{\sqrt{2}-1}{\sqrt{2}}$，
所以PC1+PQ=1+$\frac{\sqrt{2}}{2}$，
故选：A．
点评 多面体和旋转体表面上的最短距离问题的解法：求多面体表面上两点间的最短距离，一般将表面展开为平面图形，从而把它转化为平面图形内两点连线的最短长度问题．
练习册系列答案
相关题目
12．已知tanα，tanβ是方程x2+3$\sqrt{3}$x+4=0的两根，则tan（α+β）等于（ ）
| A． | -3 | B． | -$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 3 |
已知F1，F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，直线l：y=$\sqrt{2}$x+m与椭圆交于A，B两点．
19．已知函数f（x）=f（4x），当x∈[1，4）时，f（x）=lnx，若区间[1，16）内，函数g（x）=f（x）-ax有三个不同的零点，则实数a的取值范围是（ ）
| A． | （$\frac{ln2}{2}$，$\frac{1}{e}$） | B． | （$\frac{ln2}{8}$，$\frac{1}{4e}$） | C． | （$\frac{ln2}{8}$，$\frac{1}{2e}$） | D． | （$\frac{ln2}{8}$，$\frac{ln2}{4}$） |