题目内容
双曲线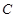 的左右焦点分别为
的左右焦点分别为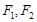 ,且
,且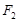 恰为抛物线
恰为抛物线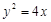 的焦点,设双曲线
的焦点,设双曲线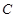 与该抛物线的一个交点为
与该抛物线的一个交点为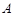 ,若
,若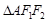 是以
是以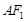 为底边的等腰直角三角形,则双曲线
为底边的等腰直角三角形,则双曲线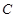 的离心率为
的离心率为
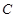 的左右焦点分别为
的左右焦点分别为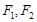 ,且
,且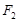 恰为抛物线
恰为抛物线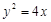 的焦点,设双曲线
的焦点,设双曲线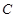 与该抛物线的一个交点为
与该抛物线的一个交点为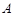 ,若
,若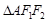 是以
是以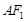 为底边的等腰直角三角形,则双曲线
为底边的等腰直角三角形,则双曲线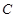 的离心率为
的离心率为A.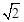 | B.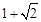 | C.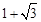 | D.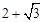 |
B
试题分析:由题意,
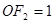 ,故
,故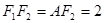 ,由双曲线的定义知,
,由双曲线的定义知,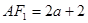 ,
,又
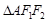 为直角三角形,故
为直角三角形,故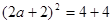 ,所以
,所以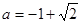 ,
,故离心率
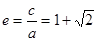 .
.点评:本题考查抛物线与双曲线的几何性质,解题的关键是正确运用双曲线及抛物线的定义,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的右焦点为
的右焦点为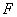 ,右准线为
,右准线为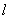 ,离心率为
,离心率为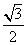 ,点
,点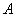 在椭圆上,以
在椭圆上,以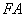 为半径的圆与
为半径的圆与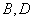 .
.
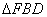 是边长为
是边长为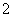 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;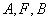 三点在同一条直线
三点在同一条直线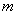 上,且原点到直线
上,且原点到直线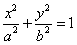 (a>b>0)的离心率为
(a>b>0)的离心率为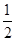 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+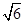 相切.
相切.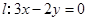 与椭圆在
与椭圆在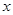 轴上方的一个交点为
轴上方的一个交点为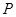 ,
,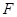 是椭圆的右焦点,试探究以
是椭圆的右焦点,试探究以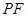 为
为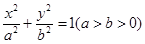 的左右焦点分别为
的左右焦点分别为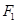 、
、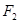 ,由4个点
,由4个点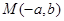 、
、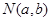 、
、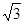 ,面积为
,面积为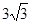 的等腰梯形.
的等腰梯形.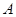 、
、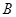 两点,求
两点,求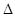
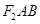 面积的最大值.
面积的最大值.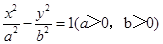 和椭圆
和椭圆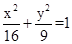 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________________.
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________________.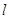 的一般方程式为
的一般方程式为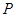 是双曲线
是双曲线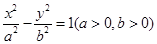 与圆
与圆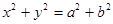 在第一象限的交点,其中
在第一象限的交点,其中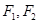 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若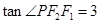 ,则双曲线的离心率为______________.
,则双曲线的离心率为______________.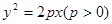 焦点的直线交抛物线于A、B两点,则
焦点的直线交抛物线于A、B两点,则 的最小值为
的最小值为 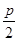 B.
B.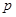 C.
C.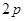 D.无法确定
D.无法确定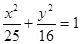 上的一点
上的一点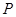 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则