Question

【题目】已知数列{an}中，a1=2，a2=6，且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列．
（1）求{an}的通项公式；
（2）记数列{ }的前n项和为Sn ， 求满足不等式Sn＞ 的n的最小值．

Answer 1

【答案】
（1）解：数列 是首项为a2﹣a1=4，公差为2的等差数列，

∴an+1﹣an=4+2（n﹣1）=2n+2（n∈N*）．

∴an=a1+（a2﹣a1）+（a3﹣a2）+…+（an﹣an﹣1）=2+4+6+…+2n=n2+n．

（2）解： ，

∴ = ，

由 得 ，n＞2015，

又n∈N*，故n的最小值为2016．

【解析】（1）利用等差数列的通项公式及其“累加求和”方法即可得出；（2）利用“裂项求和”方法、不等式的解法即可得出．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系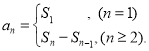)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．