题目内容
19.棱长为2的正方体的顶点都在同一个球面上,则该球的体积和表面积分别是( )| A. | $2\sqrt{3}π,12π$ | B. | $4\sqrt{3}π,12π$ | C. | $2\sqrt{3}π,6π$ | D. | $4\sqrt{3}π,6π$ |
分析 由题意,长方体的对角线是球的直径,由此得到球的半径,由球的表面积和体积公式解答.
解答 解:因为棱长为2的正方体的顶点都在同一个球面上,所以球的直径为2$\sqrt{3}$,所以半径为$\sqrt{3}$,所以球的体积为$\frac{4}{3}π(\sqrt{3})^{3}=4\sqrt{3}π$;
表面积为:$4π(\sqrt{3})^{2}=12π$;
故选B.
点评 本题考查了正方体的外接球的体积和表面积求法;关键是明确长方体的对角线是球的直径.

练习册系列答案
相关题目
11.在△ABC中,若sinA:sinB:sinC=2:3:4,则△ABC是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐三角形 | D. | 等腰直角三角形 |
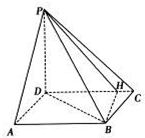 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.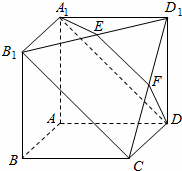 如图所示,在多面体A1B1D1-ABCD,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F
如图所示,在多面体A1B1D1-ABCD,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F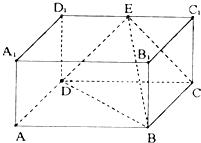 在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.
在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.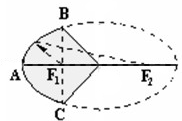 如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程.
如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程.