题目内容
4.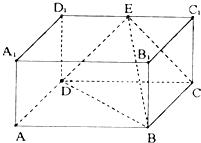 在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.
在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(Ⅰ)求证:平面EDB⊥平面EBC;
(理科生做)(Ⅱ)求二面角E-DB-C的正切值;
(文科生做)(Ⅱ)求点A到平面DBE的距离.
分析 (Ⅰ)先由BC⊥平面D1DCC1⇒BC⊥DE.再利用△DD1E为等腰直角三角形⇒∠D1ED=45°以及∠C1EC=45°可得DE⊥EC,合在一起可得平面EDB⊥平面EBC;
(理科生做)(Ⅱ)先过E在平面D1DCC1中作EO⊥DC于O⇒EO⊥面ABCD;再O在平面DBC中作OF⊥DB于F,利用三垂线定理极其逆定理可得EF⊥BD.所以∠EFO为二面角E-DB-C的平面角.再利用平面几何知识求出∠EFO的正切值即可;
(文科生做)(Ⅱ)由VE-DBA=VA-DBE,利用等体积法来求A到面EDB的距离即可.
解答 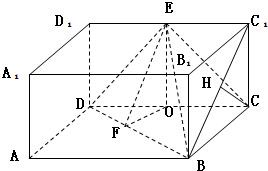 (Ⅰ)证明:在长方体ABCD-A1B1C1D1中,
(Ⅰ)证明:在长方体ABCD-A1B1C1D1中,
AB=2,BB1=BC=1,E为D1C1的中点.
∴△DD1E为等腰直角三角形,∠D1ED=45°.
同理∠C1EC=45°.
∴∠DEC=90°,即DE⊥EC.
在长方体ABCD-A1B1C1D1中,BC⊥平面D1DCC1,
又DE?平面D1DCC1,
∴BC⊥DE.又EC∩BC=C,∴DE⊥平面EBC.
∵DE?平面DEB,∵平面DEB⊥平面EBC.
(理科生做)(Ⅱ)解:如图,过E在平面D1DCC1中作EO⊥DC于O.
在长方体ABCD-A1B1C1D1中,∵面ABCD⊥面D1DCC1,∴EO⊥面ABCD.
过O在平面DBC中作OF⊥DB于F,连接EF,
∴EF⊥BD,∠EFO为二面角E-DB-C的平面角.
利用平面几何知识可得OF=$\frac{1}{\sqrt{5}}$,OE=1,tan∠EFO=$\sqrt{5}$.
∴二面角E-DB-C的正切值为$\sqrt{5}$.
(文科生做)(Ⅱ)解:设点A到平面DBE的距离为d,
∵VE-DBA=VA-DBE,
∴$\frac{1}{3}×\frac{1}{2}×1×2×1$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{3}$d
∴d=$\frac{\sqrt{6}}{3}$,
故A到面EDB的距离为$\frac{\sqrt{6}}{3}$.
点评 本题综合考查了面面垂直的判定以及二面角的求法和点到面的距离计算.在求点到面的距离时,如果直接法不好求的话,一般转化为棱锥的高利用等体积法来求.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | $2\sqrt{3}π,12π$ | B. | $4\sqrt{3}π,12π$ | C. | $2\sqrt{3}π,6π$ | D. | $4\sqrt{3}π,6π$ |
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{4}$ |
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | ($\frac{1}{4}$,$\frac{3\sqrt{3}}{4}$) | D. | (1,0) |
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |