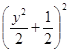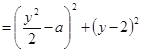题目内容
【题目】若函数f（x）= 
，则函数y=|f（x）|﹣ 
的零点个数为 ．
【答案】4
【解析】解：当x≥1时， 
= 
，即lnx= 
， 令g（x）=lnx﹣ ，x≥1时函数是连续函数，
g（1）=﹣ ＜0，g（2）=ln2﹣ 
=ln 
＞0，
g（4）=ln4﹣2＜0，由函数的零点判定定理可知g（x）=lnx﹣ ，有2个零点．
（结合函数y= 与y= 可知函数的图象由2个交点．）
当x＜1时，y=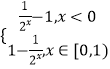 
，函数的图象与y= 的图象如图，考查两个函数由2个交点，
综上函数y=|f（x）|﹣ 的零点个数为：4个．
故答案为：4．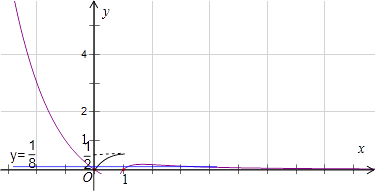
利用分段函数，对x≥1，通过函数的零点与方程根的关系求解零点个数，当x＜1时，利用数形结合求解函数的零点个数即可．
练习册系列答案
巧学巧练系列答案
相关题目
