题目内容
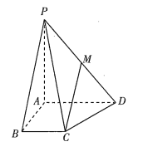
【题目】在四棱锥
中，已知
平面
，
，点
为线段
的中点．
（1）求证：
平面
；
（2）求直线
与平面
所成角的正弦值．
【答案】（1）证明见解析；（2）
【解析】
（1）取
的中点
，连接
.先利用三角形中位线的性质得到
，再根据
，得到
，则四边形
为平行四边形，进而得到
，最后利用线面平行的判定定理得到线面平行；（2）先找到直线与平面所成的角，再解三角形，从而求解．
（1）如图，取的中点，连接．
在
中，
分别为
的中点，
．
在四边形
中，
，
，
，
∴四边形为平行四边形，
，
又
平面
，
平面，
平面．
（2）过点
作
交
于点
，连接
，过点作
于点
．
平面
平面，
，又
，
平面
，
平面
，
平面
，
∴平面
平面，
又，平面
平面
，
平面，
在平面内的射影为
，
为直线与平面所成的角．
在
中，
，
，
，
∴直线与平面所成角的正弦值为．
【题目】某校从2011年到2018年参加“北约”“华约”考试而获得加分的学生（每位学生只能参加“北约”“华约”中的一种考试）人数可以通过以下表格反映出来.（为了方便计算，将2011年编号为1，2012年编号为2，依此类推）
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数 | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
（1）求这八年来，该校参加“北约”“华约”考试而获得加分的学生人数的中位数和方差；
（2）根据最近五年的数据，利用最小二乘法求出
与
之间的线性回归方程，并依此预测该校2019年参加“北约”“华约”考试而获得加分的学生人数.（结果要求四舍五入至个位）
参考公式：
.
【题目】某流行病爆发期间，某市卫生防疫部门给出的治疗方案中推荐了三种治疗药物
，
，
（，，的使用是互斥且完备的），并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示：（表中的数据都以一个疗程计）
|
|
|
|
单价（单位：元） | 600 | 1000 | 800 |
治愈率 |
|
|
|
市场使用量（单位：人） | 305 | 122 | 183 |
（Ⅰ）从感染患者中任取一人，试求其一个疗程被治愈的概率大约是多少？
（Ⅱ）试估算每名感染患者在一个疗程的药物治疗费用平均是多少.
