题目内容
【题目】在平面直角坐标系xOy中，椭圆C：
(a＞b＞0)的离心率为
，右焦点到右准线的距离为3.
（1）求椭圆C的标准方程；
（2）过点P(0，1)的直线l与椭圆C交于两点A，B.己知在椭圆C上存在点Q，使得四边形OAQB是平行四边形，求Q的坐标.
【答案】（1）
（2）Q(1，
)或(﹣1，)
【解析】
（1）结合椭圆离心率以及右焦点到右准线的距离，以及
，求得
，进而求得椭圆
的标准方程.
（2）首先判断直线
斜率不存在时，四边形
不可能是平行四边形，不符合题意.然后设出直线的方程
，联立直线的方程和椭圆方程，写出根与系数关系，求得
点坐标并代入椭圆方程，由此求得
的值，进而求得点坐标.
（1）设焦距为2c，
∵椭圆C的离心率为
，∴
①，
∵右焦点到右准线的距离为3，∴
②，
由①，②解得a＝2，c＝1，故b2＝a2﹣c2＝3，
∴椭圆C的标准方程为，
（2）当直线l斜率不存在时，四边形OAQB不可能平行四边形，故直线l斜率存在
∵直线l过点P(0，1)，设直线l为：，
设A(
，
)，B(
，
)，
由四边形OAQB是平行四边形，得Q(
，
)
，化简得：
，
，
，
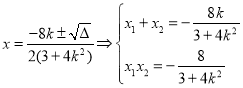∴Q(
，
)，∵点Q在椭圆C上，
∴
，解得
，代入Q的坐标，得
Q(1，)或(﹣1，).
练习册系列答案
相关题目
