题目内容
14.已知函数f(x)=x2-cosx,则f($\frac{3}{5}$),f(0),f(-$\frac{1}{2}$)的大小关系.分析 由导数判断函数f(x)在区间[0,π]上的单调性,又因f(x)是偶函数,有$f(-\frac{1}{2})=f(\frac{1}{2})$,从而判断函数值的大小.
解答 解;f′(x)=2x+sinx,当x∈[0,π]时,f′(x)>0,∴f(x)在[0,π]上单调递增,
又f(x)为偶函数,∴$f(-\frac{1}{2})=f(\frac{1}{2})$,又∵0$<\frac{1}{2}<\frac{3}{5}<π$
∴f(0)<f($-\frac{1}{2}$)<f($\frac{3}{5}$).
点评 本题考查了,函数的奇偶性,利用单调性比较函数值的大小,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.直三棱柱ABC-A1B1C1的六个顶点都在直径为$\sqrt{61}$的球面上,且AB=3,AC=4,BC=5,点D是棱BB1的中点,则该四棱锥D-ACC1A1的体积为( )
| A. | 24 | B. | 32 | C. | 36 | D. | 72 |
9.(普通中学做)如图所示,程序框图输出的某一实数对(x,y)中,若y=32,则x=( )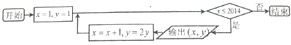
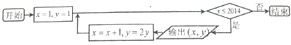
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
4.|sin165°|•cos15°-sin255°•|sin195°|的值是( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
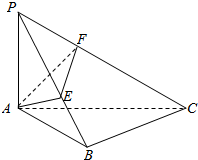 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: