题目内容
13.已知甲、乙、丙、丁四位同学,在某个时段内每人互不重复地从语文、数学、英语、文综这四个科目中选择一科进行复习.现有下面五种均为正确的说法:A.甲不在复习语文,也不在复习数学;B.乙不在复习英语,也不在复习语文;
C.丙不在复习文综,也不在复习英语;D.丁不在复习数学,也不在复习语文;
E.如果甲不在复习英语,那么丙不在复习语文.
根据以上信息,某同学判断如下:
①甲在复习英语 ②乙在复习文综 ③丙在复习数学 ④丁在复习英语
则上述所有判断正确的序号是④.
分析 根据已知中A.甲不在复习语文,也不在复习数学;B.乙不在复习英语,也不在复习语文;C.丙不在复习文综,也不在复习英语;D.丁不在复习数学,也不在复习语文;E.如果甲不在复习英语,那么丙不在复习语文.均正确,推理可得甲在复习文综,乙在复习数学,丙在复习语文,丁在复习英语,进而得到答案.
解答 解:把已知条件列表如下:
| 复习语文 | 复习数学 | 复习英语 | 复习文综 | |
| 甲 | × | × | × | √ |
| 乙 | × | √ | × | × |
| 丙 | √ | × | × | × |
| 丁 | × | × | √ | × |
故丙没有在复习数学,复习数学的只能是乙同学,故②③错误;
故乙没有在复习文综,
甲不在复习文综,丙不在复习语文,与丙在复习语文矛盾,
故甲在复习文综,丁在复习英语,
故上述判断正确的序号是:④,
故①错误,②错误;③错误;④正确;
故答案为:④
点评 这是一个典型的逻辑推理应用题,解题方法是由确定项开始用排除法,逐个推论确定各自的正确选项,最终解决问题.

练习册系列答案
相关题目
4.直三棱柱ABC-A1B1C1的六个顶点都在直径为$\sqrt{61}$的球面上,且AB=3,AC=4,BC=5,点D是棱BB1的中点,则该四棱锥D-ACC1A1的体积为( )
| A. | 24 | B. | 32 | C. | 36 | D. | 72 |
8.下列说法正确的是( )
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| B. | 若A,B,C,D是不共线的四点,则$\overrightarrow{AB}$=$\overrightarrow{DC}$是四边形ABCD是平行四边形的等价条件 | |
| C. | 若非零向量$\overrightarrow{AB}$∥$\overrightarrow{CD}$,那么AB∥CD | |
| D. | $\overrightarrow{AB}$=$\overrightarrow{CD}$的等价条件是A与C重合,B与D重合 |
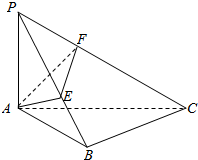 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: