题目内容
【题目】如图,某城市有一块半径为40 m的半圆形绿化区域(以O 为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
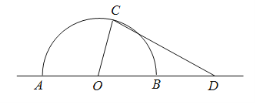
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
【答案】(1) S(x)=1600sinx+800x,0<x<π.(2) ![]()
【解析】
试题分析:(1) 根据扇形面积公式得S扇形AOC=![]() =800x ,根据三角形面积公式得S△COD=
=800x ,根据三角形面积公式得S△COD=![]() ·OC·OD·sin∠COD=1600sin(π-x)=1600sinx,从而S(x)=S△COD+S扇形AOC=1600sinx+800x,定义域为
·OC·OD·sin∠COD=1600sin(π-x)=1600sinx,从而S(x)=S△COD+S扇形AOC=1600sinx+800x,定义域为
0<x<π(2)利用导数求函数最值:先求导数S′(x)=1600cosx+800=1600(cosx+![]() ),再求导函数零点x=
),再求导函数零点x=![]() ,最后列表分析导函数符号变化规律,确定函数单调性变化规律,进而得极大值,也是最大值
,最后列表分析导函数符号变化规律,确定函数单调性变化规律,进而得极大值,也是最大值
试题解析:(1)因为扇形 AOC的半径为 40 m,∠AOC=x rad,
所以 扇形AOC的面积S扇形AOC=![]() =800x,0<x<π.
=800x,0<x<π.
在△COD中,OD=80,OC=40,∠COD=π-x,
所以△COD 的面积S△COD=![]() ·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.
·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.
从而 S=S△COD+S扇形AOC=1600sinx+800x,0<x<π.
(2)由(1)知, S(x)=1600sinx+800x,0<x<π.
S′(x)=1600cosx+800=1600(cosx+![]() ).
).
由 S′(x)=0,解得x=![]() .
.
从而当0<x<![]() 时,S′(x)>0;当
时,S′(x)>0;当![]() <x<π时, S′(x)<0 .
<x<π时, S′(x)<0 .
因此 S(x)在区间(0,![]() )上单调递增;在区间(
)上单调递增;在区间(![]() ,π)上单调递减.
,π)上单调递减.
所以 当x=![]() ,S(x)取得最大值.
,S(x)取得最大值.
答:当∠AOC为![]() 时,改建后的绿化区域面积S最大.
时,改建后的绿化区域面积S最大.

【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.