题目内容

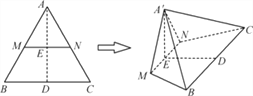
【题目】如图，等边三角形ABC的边长为4，M，N分别为AB，AC的中点，沿MN将△AMN折起，使点A到A′的位置．若平面A′MN与平面MNCB垂直，则四棱锥A′MNCB的体积为________．

【答案】3

【解析】∵ 平面A′MN与平面MNCB垂直，根据面面垂直的性质定理，可知A′E就是四棱锥A′MNCB的高，A′E＝.又四棱锥的底面面积是×＝3 ，

∴ V＝×3×＝3.

点睛:处理翻折问题关注那些量变了，那些量没有变，特别是那些没有变，在本题中，AE与MN始终保持垂直，利用面面垂直性质，可知A′E就是四棱锥A′MNCB的高，从而易得四棱锥的体积.处理多面体体积问题往往转化为三棱锥体积，而三棱锥哪个面都可以作为底面，处理体积非常灵活.

练习册系列答案
相关题目

【题目】如图1，在高为2的梯形中， ， ， ，过、分别作， ，垂足分别为、。已知，将梯形沿、同侧折起，得空间几何体，如图2。

（1）若，证明： ；

（2）若，证明： ；

（3）在（1），（2）的条件下，求三棱锥的体积。

【题目】已知数列的前n项和为Sn,点在直线上,数列为等差数列,且,前9项和为153.

(1)求数列、的通项公式;

(2)设,数列的前n项和为,求使不等式对一切的都成立的最大整数k.

【题目】公差不为零的等差数列{an}中，a3＝7，且a2，a4，a9成等比数列．

(1)求数列{an}的通项公式；

(2)设bn＝ ，求数列{bn}的前n项和Sn．

【题目】已知函数，其中为常数，为自然对数的底数．

（1）当时，求的最大值；

（2）若在区间上的最大值为，求的值．

【题目】已知中国某手机品牌公司生产某款手机的年固定成本为40万元，每生产1万部还需另投入16万元．设公司一年内共生产该款手机万部并全部销量完，每万部的销售收入为万元，且

（1）写出年利润万元关于年产量（万部）的函数解析式；

（2）当年产量为多少万部时，公司在该款手机的生产中所获得的利润最大？并求出最大利润．

【题目】已知点P（2，0），且圆C：x2+y2﹣6x+4y+4=0．

（Ⅰ）当直线过点P且与圆心C的距离为1时，求直线的方程；

（Ⅱ）设过点P的直线与圆C交于A、B两点，若|AB|=4，求以线段AB为直径的圆的方程．

【题目】设f(x)＝ (m＞0，n＞0)．

(1) 当m＝n＝1时，求证：f(x)不是奇函数；

(2) 设f(x)是奇函数，求m与n的值；

(3) 在(2)的条件下，求不等式f(f(x))＋f <0的解集．

【题目】如图，某城市有一块半径为40 m的半圆形绿化区域（以O 为圆心，AB为直径），现计划对其进行改建．在AB的延长线上取点D，OD＝80 m，在半圆上选定一点C，改建后的绿化区域由扇形区域AOC和三角形区域COD组成，其面积为S m2．设∠AOC＝x rad．

（1）写出S关于x的函数关系式S（x），并指出x的取值范围；

（2）试问∠AOC多大时，改建后的绿化区域面积S取得最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网