题目内容
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=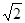 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分 .
.


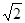 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分
 .
.

(I)证明:依题意知: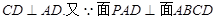


(II)由(I)知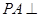 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD.在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h, 则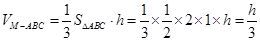
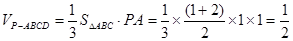
要使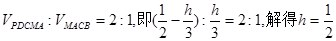
(或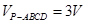 M-ABC)即M为PB的中点.
M-ABC)即M为PB的中点.
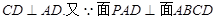


(II)由(I)知
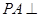 平面ABCD
平面ABCD∴平面PAB⊥平面ABCD.在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h, 则
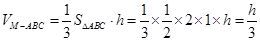
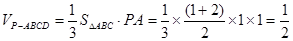
要使
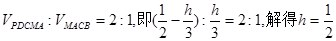
(或
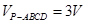 M-ABC)即M为PB的中点.
M-ABC)即M为PB的中点.略

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 中,
中, ,
, 是棱
是棱 的中点,
的中点,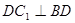


 的大小.
的大小.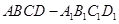 的顶点A作直线L,使L与棱
的顶点A作直线L,使L与棱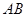 ,
,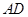 ,
,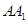 所成的角都相等,这样的直线L可以作( )
所成的角都相等,这样的直线L可以作( )
 ,E为侧棱VA的中点,则EC与底面ABCD所成角的正切值为( )
,E为侧棱VA的中点,则EC与底面ABCD所成角的正切值为( )




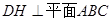 垂足为
垂足为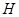 ,
,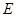 是
是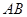 的中点且
的中点且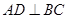 ,
,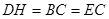 ,
,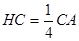 .
.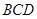
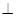 平面
平面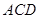 ;
;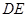 与平面
与平面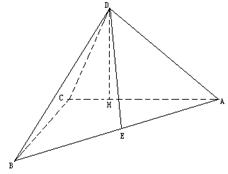
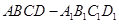 的棱
的棱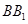 和
和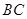 的中点分别是
的中点分别是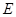 、
、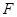 ,各棱所在直线中与直线
,各棱所在直线中与直线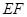 异面的直线条数是( )
异面的直线条数是( )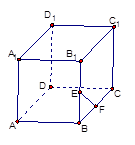
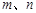 是不重合的直线,
是不重合的直线,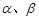 是不重合的平面,有下列命题:
是不重合的平面,有下列命题: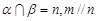 ,则
,则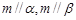 ;②若
;②若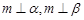 ,则
,则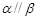 ;
;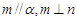 ,则
,则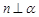 ; ④若
; ④若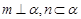 ,则
,则