题目内容
【题目】已知函数f(x)=x2+2bx+5(b∈R).
(1)若b=2,试解不等式f(x)<10;
(2)若f(x)在区间[﹣4,﹣2]上的最小值为﹣11,试求b的值;
(3)若|f(x)﹣5|≤1在区间(0,1)上恒成立,试求b的取值范围.
【答案】
(1)解:f(x)=x2+4x+5<10,
即x2+4x﹣5<0,
即(x+5)(x﹣1)<0,
解得﹣5<x<1,
故不等式的解集为(﹣5,1)
(2)解:f(x)=x2+2bx+5=(x+b)2﹣b2+5,
其对称轴为x=﹣b,
当b<﹣4时,在区间[﹣4,﹣2]上单调递增,故ymin=16﹣8x+5=﹣11,解得b=4,舍去
当﹣4≤b≤﹣2时,在对称轴处取最小值,故ymin=﹣b2+5=﹣11,解得b=﹣4,
当b>﹣2时,在区间[﹣4,﹣2]上单调递减,故ymin=4﹣4b+5=﹣11,解得b=5,
综上所述:b的值为﹣4或5
(3)解:|f(x)﹣5|≤1在区间(0,1)上恒成立,
∴|x2+bx|≤1在区间(0,1)上恒成立,
∴﹣1≤x2+2bx≤1,
∴﹣x﹣ ![]() ≤2b≤﹣x+
≤2b≤﹣x+ ![]()
∵函数y=﹣x﹣ ![]() 在(0,1)上为增函数,y>﹣1﹣1=﹣2,
在(0,1)上为增函数,y>﹣1﹣1=﹣2,
函数y=﹣x+ ![]() 在(0,1)上为减函数,y<﹣1+1=0,
在(0,1)上为减函数,y<﹣1+1=0,
∴﹣2≤2b≤0,
解得﹣1≤b≤0,
故b的取值范围为[﹣1.0]
【解析】(1)根据一元二次不等式的解法解得即可.(2)根据所给的二次函数的性质,写出对于对称轴所在的区间不同时,对应的函数的最小值,(3)利用函数的单调性分别求出y= ![]() ﹣x 的最小值为0,y=﹣x﹣
﹣x 的最小值为0,y=﹣x﹣ ![]() 的最大值为﹣2,由此求得b的取值范围.
的最大值为﹣2,由此求得b的取值范围.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 名校课堂系列答案
名校课堂系列答案【题目】某农科所发现,一种作物的年收获量 ![]() (单位:
(单位: ![]() )与它“相近”作物的株数
)与它“相近”作物的株数 ![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 ![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为 ![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求该作物的年收获量 ![]() 关于它“相近”作物的株数
关于它“相近”作物的株数![]() 的线性回归方程;
的线性回归方程;
(2)农科所在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每
个小正方形的面积为 ![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
获量以线性回归方程计算所得数据为依据)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估
计分别为, 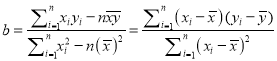 ,
, ![]()