题目内容
【题目】已知函数f(x)=log22x﹣mlog2x+2,其中m∈R.
(1)当m=3时,求方程f(x)=0的解;
(2)当x∈[1,2]时,求f(x)的最小值.
【答案】
(1)解:令t=log2x,则当m=3时,方程f(x)=0可化为:t2﹣3t+2=0,解得:t=1或t=2
所以x=2或x=4
(2)解:令t=log2x,x∈[1,2],
则t∈[0,1],y=t2﹣mt+2,
其图象开口朝上,且以直线x= ![]() 为对称轴;
为对称轴;
①当 ![]() <0,即m=0时,
<0,即m=0时,
则t=0,即x=1时,f(x)min=2;
②当0≤ ![]() ≤1,即0≤m≤2时,
≤1,即0≤m≤2时,
则t=m,即x=2m时,f(x)min= ![]() +2;
+2;
③当 ![]() >1,即m>2时,
>1,即m>2时,
则t=1,即m=2时,f(x)min=3﹣m;
综上f(x)min= 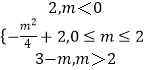
【解析】(1)令t=log2x,则当m=3时,方程f(x)=0可化为:t2﹣3t+2=0,解得答案;(2)令t=log2x,x∈[1,2],则t∈[0,1],y=t2﹣mt+2,结合二次函数的图象和性质,可得答案.
【考点精析】关于本题考查的二次函数的性质和二次函数在闭区间上的最值,需要了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;当
上递减;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目

