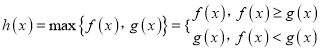题目内容
【题目】已知函数f(x)= ![]() ,x∈R,a∈R.
,x∈R,a∈R.
(1)a=1时,求证:f(x)在区间(﹣∞,0)上为单调增函数;
(2)当方程f(x)=3有解时,求a的取值范围.
【答案】
(1)证明:a=1时,f(x)= ![]() ,
,
x<0时,f(x)= ![]() ,
,
令x1<x2<0,
则f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵x1<x2<0,
∴(1﹣x1)(1﹣x2)>0,x1﹣x2<0,
∴f(x1)<f(x2),
∴f(x)在区间(﹣∞,0)上为单调增函数
(2)解:由f(x)= ![]() =3,
=3,
得:ax=3|x|+2,
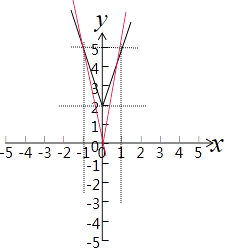
画出函数y=ax和y=3|x|+2的图象,如图示:
 ,
,
结合图象,a>3或a<﹣3.
【解析】(1)求出f(x)的解析式,根据函数单调性的定义证明即可;(2)问题转化为函数y=ax和y=3|x|+2有交点,从而求出a的范围即可.
【考点精析】利用函数单调性的判断方法对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.

练习册系列答案
相关题目
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?