题目内容
【题目】已知椭圆![]() :
:![]()
![]() 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)椭圆上的任一点到焦点的距离最大值为![]() ,结合离心率的值即可得方程;
,结合离心率的值即可得方程;
(2)设![]() ,
, ![]() ,直线
,直线![]() 与圆
与圆![]() :
: ![]() 的交点为
的交点为![]() ,①当直线
,①当直线![]() 轴时,
轴时, ![]() ,易得
,易得![]() ,②当直线
,②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,与椭圆联立得得
,与椭圆联立得得![]() ,
, ![]() ,结合韦达定理可解得
,结合韦达定理可解得![]() ,
, ![]() 即可得最值.
即可得最值.
试题解析:
(1)椭圆上的任一点到焦点的距离最大值为![]() ,又离心率为
,又离心率为![]() ,
,
解得: ![]() ,进而得
,进而得![]() .
.
椭圆![]() 的方程为:
的方程为: ![]()
(2)设![]() ,
, ![]() ,直线
,直线![]() 与圆
与圆![]() :
: ![]() 的交点为
的交点为![]() .
.
①当直线![]() 轴时,
轴时, ![]() ,
,
由 得
得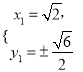 或
或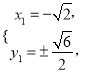
此时可求得![]() .
.
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
联立 消
消![]() 得
得![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
所以![]()
![]() ,
,
由![]() 得
得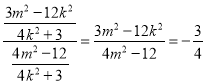 ,
, ![]()
此时![]() .
.
圆![]() :
: ![]() 的圆心到直线
的圆心到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
得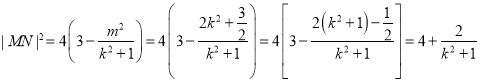 ,
,
所以当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() ,
,
综合①②知,直线![]() 被圆
被圆![]() :
: ![]() 截得弦长的最大值为
截得弦长的最大值为![]() ,
,
此时,直线![]() 的方程为
的方程为![]()
点睛: 本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.

 阅读快车系列答案
阅读快车系列答案【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
按分层抽样抽取10只,再随机抽取3只品尝,记![]() 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.

