题目内容
双曲线
-
=1(a>0,b>0)的离心率是2,则渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、3x±y=0 | ||
B、x±
| ||
| C、x±3y=0 | ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由离心率是2得c=2a,代入c2=a2+b2得3a2=b2,求出
的值,再求出双曲线的渐近线方程.
| b |
| a |
解答:
解:由题意得,
=2,则即
=
,
所以双曲线
-
=1的渐近线方程为y=±
x=±
x,
即
x±y=0,
故选:D.
| c |
| a |
| b |
| a |
| 3 |
所以双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| 3 |
即
| 3 |
故选:D.
点评:本题考查双曲线的标准方程以及简单的几何性质,属于中档题.

练习册系列答案
相关题目
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )| A、y2=2x |
| B、y2=4x |
| C、y2=8x |
| D、y2=16x |
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
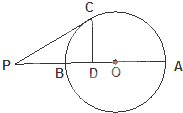 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=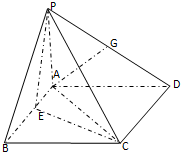 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.