题目内容
函数f(x)=(1+x)2-ln(1+x)的单调区间为 .
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的定义域,求出函数的导数,通过导数与0的关系,求出x的范围即可.
解答:
解:函数f(x)=(1+x)2-ln(1+x)的定义域为(-1,+∞),
∵f′(x)=2(x+1)-
=
,
令f′(x)=0,解得x=-1+
,
当f′(x)>0时,即x>-1+
时,函数f(x)单调递增,
当f′(x)<0时,即-1<x<-1+
时,函数f(x)单调递减,
故函数f(x)=(1+x)2-ln(1+x)在(-1,-1+
)上单调递减,在(-1+
,+∞)上单调递增.,
故答案为:单调减区间为(-1,-1+
),单调增区间为(-1+
,+∞).
∵f′(x)=2(x+1)-
| 1 |
| x+1 |
| 2(x+1)2-1 |
| x+1 |
令f′(x)=0,解得x=-1+
| ||
| 2 |
当f′(x)>0时,即x>-1+
| ||
| 2 |
当f′(x)<0时,即-1<x<-1+
| ||
| 2 |
故函数f(x)=(1+x)2-ln(1+x)在(-1,-1+
| ||
| 2 |
| ||
| 2 |
故答案为:单调减区间为(-1,-1+
| ||
| 2 |
| ||
| 2 |
点评:本题考查函数的对数求解函数的单调区间的方法,函数的定义域是易错点,易因为忘记求定义域导致错误,考查计算能力.

练习册系列答案
相关题目
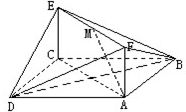 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
(1)求证:AM∥平面BDE;
(2)求证:AM⊥平面BDF;
(3)求三棱锥M-BDE的体积VM-BDE.
已知双曲线
-
=1的左右焦点分别为F1、F2,O为双曲线的中心,P是双曲线右支上的点△PF1F2的内切圆的圆心为I,且圆I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,则|OA|•|OB|=( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、3 | B、9 | C、25 | D、16 |
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )