题目内容
【题目】如图,在四凌锥S﹣ABCD中,底面ABCD是直角梯形,AD∥BC,SA⊥CD,AB⊥平面SAD,M是SC的中点,且SA=AB=BC=2,AD=1. 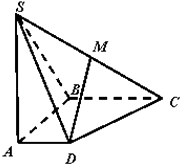
(1)求证:DM∥平面SAB;
(2)求四棱锥S﹣ABCD的体积.
【答案】
(1)证明:如图,
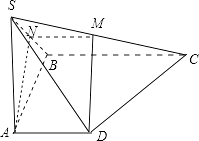
取SB的中点N,连接AN、MN,
∵点M是SC的中点,∴MN∥BC,且BC=2MN,
∵底面ABCD是直角梯形,AB垂直于AD,AB⊥BC,BC=2,AD=1,
∴AD∥BC,且BC=2AD,∴MN∥AD,且MN=AD,
∴四边形MNAD是平行四边形,∴DM∥AN,
∵DM面SAB,AN面SAB,∴DM∥平面SAB
(2)解:∵AB⊥底面SAD,SA底面SAD,AD底面SAD,
∴AB⊥SA,AB⊥AD,∵SA⊥CD,AB、CD是平面ABCD内的两条相交直线,
∴侧棱SA⊥底面ABCD,又在四棱锥S﹣ABCD中,侧棱SA⊥底面ABCD,
底面ABCD是直角梯形,AD∥BC,AB⊥AD,SA=AB=BC=2,AD=1,
∴ ![]()
【解析】(1)要证DM∥平面SAB,可取SB的中点N,连接AN、MN,利用中位线知识及已知条件证明四边形MNAD是平行四边形,从而得到DM∥AN,由线面平行的判定得证;(2)由AB⊥平面SAD,结合线面垂直的性质得到SA⊥AB,再由已知SA⊥CD,利用线面垂直的判定得SA⊥底面ABCD,由直角梯形的面积公式求出底面积,直接代入棱锥体积公式得答案.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

练习册系列答案
相关题目