[题目]某地区拟建立一个艺术博物馆.采取竞标的方式从多家建筑公司选取一家建筑公司.经过层层筛选.甲.乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从个招标问题中随机抽取个问题.已知这个招标问题中.甲公司可正确回答其中的道題目.而乙公司能正确回答毎道题目的概率均为.甲.乙两家公司对每题的回答都是相互题目和参考答案——青夏教育精英家教网—

题目内容

【题目】某地区拟建立一个艺术博物馆，采取竞标的方式从多家建筑公司选取一家建筑公司，经过层层筛选，甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从个招标问题中随机抽取个问题，已知这个招标问题中，甲公司可正确回答其中的道題目，而乙公司能正确回答毎道题目的概率均为，甲、乙两家公司对每题的回答都是相互独立，互不影响的.

（1）求甲、乙两家公司共答对道题目的概率；

（2）请从期望和方差的角度分析，甲、乙两家哪家公司竞标成功的可能性更大？

【答案】（1）（2）甲公司竞标成功的可能性更大.

【解析】试题分析：（1）分两种情况求概率：甲答对道题、乙答对道题；甲答对道题、乙答对道题；其中甲答对道题概率为, 乙答对道题概率为，最后根据概率乘法公式与加法公式求概率，（2）分别求甲、乙公司正确完成面试的题数期望和方差，期望较大、方差较小的公司竞标成功的可能性更大.先确定随机变量可能取法，求出对应概率(甲答对道题概率为, 乙答对道题概率为)，利用期望公式及方差公式求期望与方差.

试题解析：（1）由题意可知，所求概率.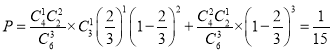

(2)设甲公司正确完成面试的题数为,则的取值分别为，， .

, ， .

则的分布列为：

设乙公司正确完成面试的题为,则取值分别为，，， .

, ,

则的分布列为：

.（或,）

.( )

由, 可得，甲公司竞标成功的可能性更大.

练习册系列答案

（1）求居民月用水量费用（单位：元）关于月用电量（单位：吨）的函数解析式；

（2）为了了解居民的用水情况，通过抽样，获得今年3月份100户居民每户的用水量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年3月份用水费用不超过16元的占60%，求的值；

（3）若地区居民用水量平均值超过6吨，则说明该地区居民用水没有节约意识在满足（2）的条件下，请你估计市居民用水是否有节约意识（同一组中的数据用该组区间的中点值作代表）.

【题目】点E、F、G分别是正方体ABCD－A1B1C1D1的棱AB、BC、B1C1的中点，如图所示，则下列命题中的真命题是________(写出所有真命题的编号)．

①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形；

②过点F、D1、G的截面是正方形；

③点P在直线FG上运动时，总有AP⊥DE；

④点Q在直线BC1上运动时，三棱锥A－D1QC的体积是定值；

⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点，则点M的轨迹是一条线段．

【题目】（本小题10分）从3名男生和名女生中任选2人参加比赛。

①求所选2人都是男生的概率;

②求所选2人恰有1名女生的概率;

③求所选2人中至少有1名女生的概率

【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50]，[50，60]，…，[80，90]，[90，100]

（1）求频率分布图中a的值；
（2）估计该企业的职工对该部门评分不低于80的概率；
（3）从评分在[40，60]的受访职工中，随机抽取2人，求此2人评分都在[40，50]的概率．

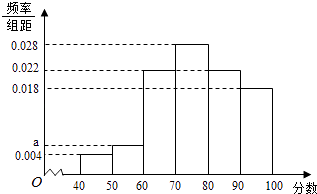
【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示：

组号	分组	频数	频率
第1组
第2组		①
第3组		20	②
第4组		20
第5组		10
合计		100

（1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图（用阴影表示）；

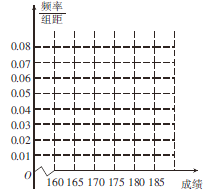
（2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；

（3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受考官进行面试，求：第4组至少有一名选手被考官面试的概率.

【题目】在△ABC中，内角A，B，C对边的边长分别是a，b，c，已知c=2，C= ．
（1）若△ABC的面积等于，求a，b；
（2）若sinC+sin（B﹣A）=2sin2A，求△ABC的面积．

【题目】在平面直角坐标系xOy中，已知定点A(－4，0)、C(4，0)，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为 r.

(1)求圆M的方程；（2)当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．

【题目】如图，在矩形ABCD中，AB=1，AD= ，P矩形内的一点，且AP= ，若 =λ +μ ，（λ，μ∈R），則λ+ μ的最大值为．

试题分类