题目内容
已知:函数f(x)满足f(1)=1,f(2)=4
(1)符合上述条件的函数f(x)有多少个?
(2)写出三个符合上述条件的函数;
(3)是否存在满足上述条件的形式为y=4x-
的函数?如果存在,求出这样的函数,并求出该函数的值域;如果不存在,请说明理由.
(1)符合上述条件的函数f(x)有多少个?
(2)写出三个符合上述条件的函数;
(3)是否存在满足上述条件的形式为y=4x-
| ax+b |
(1)函数f(x)上只知道两点,故函数不能确定,符合上述条件的函数f(x)有无数个;
(2)若f(x)为一次函数,可由两点式直接写出直线方程即f(x)=3x-2,
若f(x)为二次方程,设f(x)=ax2+bx+c,由条件
,
得3a+b=3,a、b取一些特值即可.如:f(x)=x2,f(x)=2x2-3x+2等.
(3)假设存在,则
,解得
,故y=4x-
令
=t(t≥0),则x=
,则原函数变为y=
t2-t-
(t≥0)
当t=
时,函数有最小值-
所以函数的值域为[-
,+∞)
(2)若f(x)为一次函数,可由两点式直接写出直线方程即f(x)=3x-2,
若f(x)为二次方程,设f(x)=ax2+bx+c,由条件
|
得3a+b=3,a、b取一些特值即可.如:f(x)=x2,f(x)=2x2-3x+2等.
(3)假设存在,则
|
|
| 7x+2 |
令
| 7x+2 |
| t2-2 |
| 7 |
| 4 |
| 7 |
| 8 |
| 7 |
当t=
| 7 |
| 8 |
| 163 |
| 112 |
所以函数的值域为[-
| 163 |
| 112 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
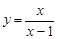 ,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线
,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线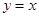 对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数
对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数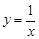 的图象重合。其中正确命题的序号是---------------。
的图象重合。其中正确命题的序号是---------------。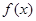 在区间(0,+∞)上是减函数,那么
在区间(0,+∞)上是减函数,那么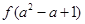 与
与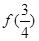 的大小关系是( ).
的大小关系是( ).



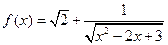 的值域是 .
的值域是 . 