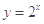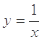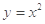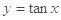题目内容
已知函数f(x)=(
+
)•x.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求证:f(x)>0.
| 1 |
| 2x-1 |
| 1 |
| 2 |
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求证:f(x)>0.
(1)由2x-1≠0得x≠0,∴函数f(x)的定义域为(-∞,0)∪(0,+∞)
(2)∵f(x)=(
+
)•x=
•x
∴f(-x)=
•(-x)=-x•
=-x•
=-
•x=f(x)
∴函数f(x)为定义域上的偶函数.
(3)证明:当x>0时,2x>1
∴2x-1>0,
∴
>0,
∴(
+
)•x>0
∵f(x)为定义域上的偶函数
∴当x<0时,f(x)>0
∴f(x)>0成立
(2)∵f(x)=(
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 2x+1 |
| 2(2x-1) |
∴f(-x)=
| 2-x+1 |
| 2(2-x-1) |
| ||
2(
|
| 1+2x |
| 2(1-2x) |
| 2-x+1 |
| 2(2-x-1) |
∴函数f(x)为定义域上的偶函数.
(3)证明:当x>0时,2x>1
∴2x-1>0,
∴
| 1 |
| 2x-1 |
∴(
| 1 |
| 2x-1 |
| 1 |
| 2 |
∵f(x)为定义域上的偶函数
∴当x<0时,f(x)>0
∴f(x)>0成立

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
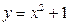 的函数的个数
的函数的个数 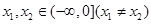 ,
,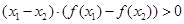 ,则当n∈N﹡时,有( ).
,则当n∈N﹡时,有( ).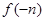 <
<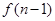 <
<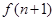
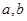 ,记
,记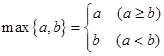 ,若
,若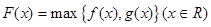 ,其中奇函数
,其中奇函数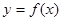 在
在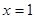 时有极小值
时有极小值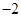 ,
,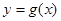 是正比例函数,
是正比例函数,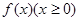 与
与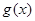 图象如图,则下列关于
图象如图,则下列关于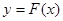 的说法中正确的是( )
的说法中正确的是( )
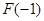 和极小值
和极小值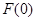
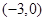 上是增函数
上是增函数