题目内容
14.已知函数f(x)=3sin($\frac{x}{2}$+$\frac{π}{6}$)+3(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出f(x)的周期、振幅、初相、对称轴;
(3)求此函数的最大值、最小值及相对应自变量x的集合;
(4)说明此函数图象可由y=sinx的图象经怎样的变换得到.
分析 (1)利用五点法,可得函数的图象;
(2)利用函数解析式可知周期、振幅、初相、对称轴;
(3)利用函数的图象,可得f(x)最值及x的集合.
(4)利用三角函数图象变换规律,可得结论
解答 解:(1)列表如下:
| x | $-\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{x}{2}+\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 3 | 6 | 3 | 0 | 3 |
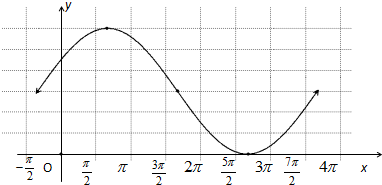 …(5分);
…(5分);(2)∴其周期T=$\frac{2π}{\frac{1}{2}}=4π$,振幅A=3,初相φ=$\frac{π}{6}$,由($\frac{x}{2}$+$\frac{π}{6}$)=kπ+$\frac{π}{2}$(k∈Z),得x=2kπ+$\frac{2π}{3}$(k∈Z)即为对称轴
(3)当sin($\frac{x}{2}$+$\frac{π}{6}$)=1时函数的最大值为3+3=6,此时($\frac{x}{2}$+$\frac{π}{6}$)=2kπ+$\frac{π}{2}$(k∈Z),解得x的集合为{x|x=4kπ+$\frac{2π}{3}$,k∈Z};
当sin($\frac{x}{2}$+$\frac{π}{6}$)=-1时,函数的最小值为-3+3=0;此时($\frac{x}{2}$+$\frac{π}{6}$)=2kπ-$\frac{π}{2}$(k∈Z),解得x 的集合为{x|x=4kπ-$\frac{4π}{3}$,k∈Z}…(8分);
(4)①由y=sinx的图象上各点向左平移ϕ=$\frac{π}{6}$个长度单位,得y=sin(x+$\frac{π}{6}$)的图象;
②由y=sin(x+$\frac{π}{6}$)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得y=sin($\frac{x}{2}$+$\frac{π}{6}$)的图象;
③由y=3sin($\frac{x}{2}$+$\frac{π}{6}$)的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得y=3sin($\frac{x}{2}$+$\frac{π}{6}$)的图象;
④由y=3sin($\frac{x}{2}$+$\frac{π}{6}$)的图象上各点向上平移3个长度单位,得y=3sin($\frac{x}{2}$+$\frac{π}{6}$)+3的图象.
点评 本题考查用五点法作图,着重考查正弦函数的性质与作图能力,考查三角函数的图象与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.已知两个不同的平面α,β和两条不重合的直线m,n,则下列命题正确的是( )
| A. | 若m∥n,n?α,则m∥α | B. | 若α⊥β,α∩β=n,m⊥n,则m⊥β | ||
| C. | 若m?α,n?α,m∥β,n∥β,则α∥β | D. | 若m⊥β,m?α,则α⊥β |
 如图把椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…P7七个点,F是椭圆的一个焦点,则|P1F|+|P2F|+…+|P7F|=28.
如图把椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…P7七个点,F是椭圆的一个焦点,则|P1F|+|P2F|+…+|P7F|=28. 如图ABCD为正方形,VD⊥平面ABCD,VD=AD=2,F为VA中点,E为CD中点.
如图ABCD为正方形,VD⊥平面ABCD,VD=AD=2,F为VA中点,E为CD中点.