题目内容
19．已知向量$\overrightarrow{a}$=（1，3），$\overrightarrow{b}$=（2，0），若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$+λ$\overrightarrow{b}$垂直，则λ的值等于（ ）| A． | -6 | B． | -2 | C． | 6 | D． | 2 |
分析 先求出得$\overrightarrow{a}$+$\overrightarrow{b}$ 和$\overrightarrow{a}$+λ$\overrightarrow{b}$的坐标，再根据（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{a}$+λ$\overrightarrow{b}$）=0，求得λ的值．
解答 解：由题意可得$\overrightarrow{a}$+$\overrightarrow{b}$=（3，3），$\overrightarrow{a}$+λ$\overrightarrow{b}$=（1+2λ，3），
∵$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$+λ$\overrightarrow{b}$垂直，∴（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{a}$+λ$\overrightarrow{b}$）=（3，3）•（1+2λ，3）=3+6λ+9=0，
求得λ=-2，
故选：B．
点评 本题主要考查两个向量垂直的性质，两个向量坐标形式的运算，属于基础题．
练习册系列答案
相关题目
9．已知复数z1=4-mi，z2=6m+ni，且m、n∈R，若z2=z12，则实数n=（ ）
| A． | -2，8 | B． | 2，-8 | C． | 64，-16 | D． | 16，-64 |
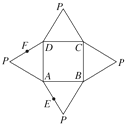如图是一几何体的平面展开图，其中ABCD为正方形，E，F分别为PA，PD的中点．在此几何体中，给出下面四个结论：