题目内容

6．如图把椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的长轴AB分成8分，过每个分点作x轴的垂线交椭圆的上半部分于P1，P2，…P7七个点，F是椭圆的一个焦点，则|P1F|+|P2F|+…+|P7F|=28．

分析 分别连结点F2与P1，P2，…P7七个点，利用对称性计算即得结论．

解答 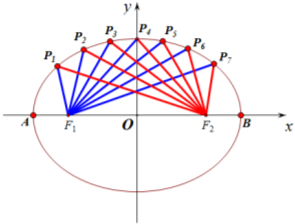解：F是椭圆的一个焦点，不妨令F为左焦点F1，则右焦点为F2，
分别连结点F2与P1，P2，…P7七个点，
易知当i+j=8时有：|PiF1|=|PjF2|，其中i、j∈{1，2，3，…，7}，
由椭圆定义可知：|PiF1|+|PiF2|=2a=2×4=8，i∈{1，2，3，…，7}，
∴2（|P1F|+|P2F|+…+|P7F|）=7×8=56，
即|P1F|+|P2F|+…+|P7F|=28，
故答案为：28．

点评 本题考查椭圆的定义，利用对称轴是解决本题的关键，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
16．已知椭圆的中心在坐标原点，焦点在坐标轴上，离心率为$\frac{\sqrt{3}}{2}$，且经过点（2，0），求这个椭圆的方程．
17．椭圆方程为9x2+4y2=36，P为椭圆上任一点，F1，F2为焦点，则|PF1|+|PF2|=（　　）
A．2B．3C．4D．6
14．已知函数f（x）=3sin（$\frac{x}{2}$+$\frac{π}{6}$）+3
（1）用五点法画出它在一个周期内的闭区间上的图象；

（2）指出f（x）的周期、振幅、初相、对称轴；
（3）求此函数的最大值、最小值及相对应自变量x的集合；
（4）说明此函数图象可由y=sinx的图象经怎样的变换得到．
1．已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a≥2b＞0），则椭圆C的离心率的取值范围是[$\frac{\sqrt{3}}{2}$，1）．
11．已知P是椭圆$\frac{x^2}{4}+\frac{y^2}{3}$=1上的点，F1，F2分别是椭圆的左、右焦点，若∠F1PF2=$\frac{π}{3}$，则△F1PF2的面积为$\sqrt{3}$．
18．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与直线x+y-1=0相交于A，B两点，且线段AB的中点在直线y=x上．
（Ⅰ）求椭圆的离心率；
（Ⅱ）若椭圆的右焦点关于直线y=$\frac{1}{2}$x的对称点的横坐标为x0=$\frac{6}{5}$，求椭圆的方程．
15．已知等比数列{an}满足q＞1，且a1+a6=11，a3a4=$\frac{32}{9}$．
（1）求数列{an}的通项公式；
（2）是否存在正整数m，恰使$\frac{2}{3}$am-1，am2，am+1+$\frac{4}{9}$这三个数依次成等差数列，若存在，求出m的值；若不存在，说明理由．
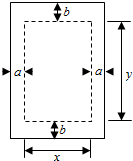16．如图，一份印刷品的排版面积（虚线边框矩形）为4000cm2，它的两边都留有宽为a（单位：cm）的空白，顶部和底部都留有宽为b（单位：cm）的空白，已知a，b的值分别为4和10．
（1）若设虚线边框矩形的长为x（单位：cm），宽为y（单位：cm），求纸的用量S（x）关于x的函数解析式；
（2）要使纸的用量最少，x，y的值应分别为多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网